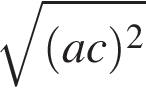равен?
1) 
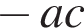
2) 
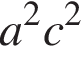
3) 
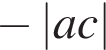
4) 
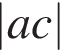
5) 
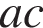
Решение. Поскольку 
то и 
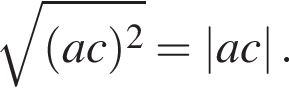
Правильный ответ указан под номером 4.
Ответ: 4
291
4
РЕШУ ЕНТ — математика
Вариант № 10
Реальная версия ЕНТ по математике 2021 года. Вариант 4126
1.
i
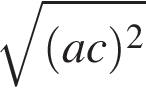равен?
1)
2)
3)
4)
5)
2.
i
Решить уравнение: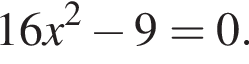 
1) 4 и −4
2) 3 и −3
3) 
и 
и 4) 
и 
и 5) 3 и −3
3.
i
Решите систему уравнений: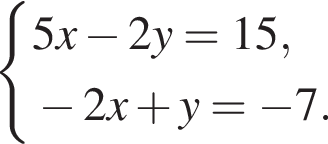 
1) (3; 0)
2) (0; −7,5)
3) (1; 3)
4) (1; −5)
5) (0; 3,5)
Подставляя это выражение в первое уравнение, получаем 
Итого, ответ (1; −5).4.
i
Токарь, делая по 54 детали в час, изготовил все детали за 5 часов. За сколько часов токарь изготовит все детали, если будет делать по 15 деталей в час?
1) 15 ч
2) 18 ч
3) 9 ч
4) 16 ч
5) 12 ч
деталей. Работая со скоростью 15 деталей в час, он потратил бы на работу 
часов.5.
i
Найдите область определения функции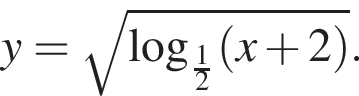 
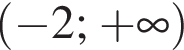
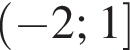
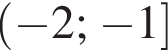
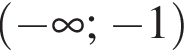
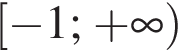
1) 
2) 
3) 
4) 
5) 
знак неравенства меняется. Тогда 
6.
i
Решите систему неравенств: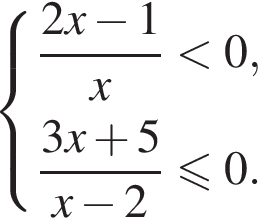 
1) (0; 0,5)
2) [−0,6; 0,5)
3) [0; 0,5]
4) 
5) (0,5; 2]
корнем знаменателя 
При 
или 
числитель и знаменатель имеют одинаковые знаки (такие x не подходят), при 
числитель отрицателен, а знаменатель положителен (такие x подходят), при 
дробь равна нулю, а при 
—
При всех 
во втором неравенстве числитель дроби положителен, а знаменатель отрицателен, поэтому все такие числа являются решениями и второго неравенства.7.
i
Найдите первый член арифметической прогрессии, если сумма двадцати яти первых членов прогрессии равна 250 и 
1) 23,5
2) −24
3) −26
4) −20,5
5) 22,5
8.
i
Найдите область значений квадратичной функции: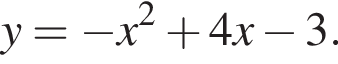 
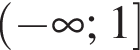
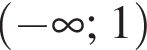
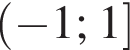
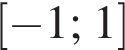
1) 
2) 
3) 
4) 
5) 
имеет корни в точности при тех a, при которых имеет корни уравнение 
то есть при тех, при которых дискриминант этого последнего уравнения неотрицателен. Решая неравенство 
Это и есть область значений функции.9.
i
Из круга радиусом 10 вырезали квадрат наибольшего размера. Площадь оставшейся части круга при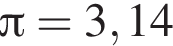 
равна
1) 212
2) 126
3) 38
4) 145
5) 114
Тогда сторона его равна 
площадь 
а площадь оставшейся части круга 
10.
i
Найдите диагональ прямоугольной призмы, в основании которой лежит прямоугольник со сторонами 8 см и 
см
1) 15 см
2) 11 см
3) 14 см
4) 13 см
5) 12 см
5 см. Поэтому его диагональ имеет длину 
11.
i
Числовая последовательность задана условиями 
Какое из указанных чисел равно x3?
1) −3
2) 1
3) −2
4) 0
5) −1
находим 
При 
находим 
12.
i
Значение переменной х, при котором верно неравенство: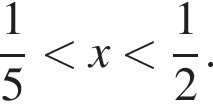 
1) 
2) 
3) 
4) 
5)
и 
будет лежать 
но не будут 
13.
i
Решите систему неравенств: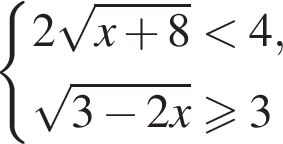 
и укажите количество целых решений системы неравенств.
1) 2
2) 1
3) 5
4) 3
5) 4
При таких значениях x поделим неравенство на 2 и возведем в квадрат. Получим 
На этом промежутке 4 целых числа: −8; −7; −6; −5.14.
i
Вычислите объем фигуры, получаемой вращением вокруг оси Ox дуги кривой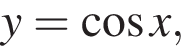 
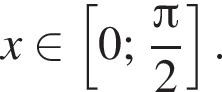
1) 
2) 
3) 
4) 
5) 
15.
i
Сторона ромба равна 12. Косинус одного из его углов равен 
Площадь ромба равна
1) 40
2) 48
3) 
4) 
5) 
16.
i
Вычислите: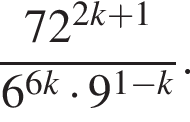 
1) 
2) 6
3) 
4) 8
5) 4
17.
i
На рисунке радиусы касающихся окружностей с центрами O1 и O2 равны 7 и 3. К окружностям проведена общая касательная BC. Расстояние между точками касания равно:
1) 
2) 
3) 
4) 
5) 
18.
i
Моторная лодка прошла 21 км по течению реки и обратно, затратив 2 ч 40 мин. в другой раз та же моторная лодка прошла по течению реки 18 км и 14 км против течения реки, затратив на весь путь 2 ч. Какова собственная скорость лодки?
1) 10 км/ч
2) 18 км/ч
3) 16 км/ч
4) 2 км/ч
5) 12 км/ч
19.
i
Решите систему неравенств: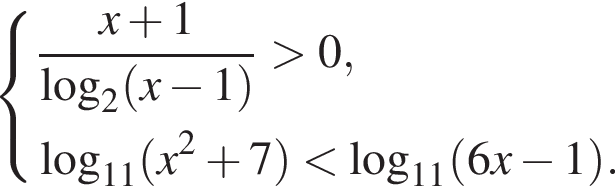 
1) 
2) 
3) 
4) 
5) 
(поскольку 
при всех x), то есть 
20.
i
Из точки M проведен перпендикуляр MK, равный 6 см к плоскости квадрата ACPK. Наклонная MC образует с плоскостью квадрата угол 60°. Найдите сторону квадрата.
1) 3 см
2) 
см
см3) 
см
см4) 6 см
5) 
см
см
раз меньше его диагонали, сторона равна 
21.
i
Учитель дал домашнее практическое задание по геометрии. Сделать макет призмы и составить к ним задания. Самат подготовил макет правильной шестиугольной призмы со стороной основания равной 1, а боковое ребро 2 и составил следующие задания.
Найдите сумму векторов 
и 
1) 
2) 
3) 
4) 
5) 
22.
i
Учитель дал домашнее практическое задание по геометрии. Сделать макет призмы и составить к ним задания. Самат подготовил макет правильной шестиугольной призмы со стороной основания равной 1, а боковое ребро 2 и составил следующие задания.
Определите длину полученного вектора.
1) 
2) 
3) 
4)
5) 1
23.
i
Учитель дал домашнее практическое задание по геометрии. Сделать макет призмы и составить к ним задания. Самат подготовил макет правильной шестиугольной призмы со стороной основания равной 1, а боковое ребро 2 и составил следующие задания.
Определите вектор, равный сумме векторов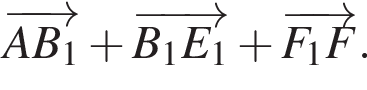 
1)
2)
3)
4) 
5)
24.
i
Учитель дал домашнее практическое задание по геометрии. Сделать макет призмы и составить к ним задания. Самат подготовил макет правильной шестиугольной призмы со стороной основания равной 1, а боковое ребро 2 и составил следующие задания.
Определите угол между прямой AD1 и плоскостью ABCDEF.
1) 30°
2) 90°
3) 60°
4) 180°
5) 45°
25.
i
Учитель дал домашнее практическое задание по геометрии. Сделать макет призмы и составить к ним задания. Самат подготовил макет правильной шестиугольной призмы со стороной основания равной 1, а боковое ребро 2 и составил следующие задания.
Определите угол между векторами 
и 
1) 60°
2) 180°
3) 90°
4) 45°
5) 30°
поэтому 
26.
i
Среди натуральных чисел от 32 до 42 включительно выберите те числа, которые имеют больше 5 делителей (кроме 1 и самого числа).
1) 33
2) 42
3) 32
4) 40
5) 34
6) 35
7) 38
8) 36
то число имеет 
делителей, включая единицу и само число. Рассмотрим предложенные варианты: 
имеет четыре делителя;
имеет восемь делителей;
имеет шесть делителей;
имеет восемь делителей;
имеет четыре делителя;
имеет четыре делителя;
имеет четыре делителя;
имеет девять делителей.27.
i
Корнями уравнения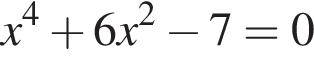 
являются?
1) 6
2) 7
3) −6
4) 1
5) −7
6) 4
7) −4
8) −1
что невозможно, либо 
откуда 
28.
i
Какому промежутку принадлежит отношение 
где (x; y) — решение системы уравнений: 
1) (−3; 3)
2) (4; 7)
3) (2; 7)
4) (0; 3)
5) [−3; 5]
6) [−1; 1]
7) [2; 5]
8) [3; 5]
и рассмотрим систему 
и 
Тогда второе уравнение дает 
и 
откуда 
и 
29.
i
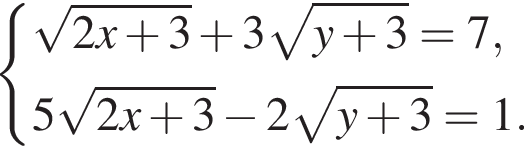
Смешали 50% и 70% растворы кислоты и получили 65% раствор. В каких пропорциях их смешали?
1) 1:2
2) 2:9
3) 2:7
4) 1:1
5) 1:4
6) 2:3
7) 1:3
8) 2:5
литров кислоты. Значит, 
30.
i
Укажите все решения неравенства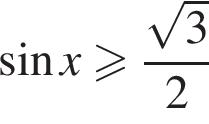 
на интервале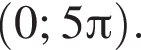 
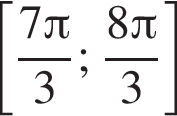
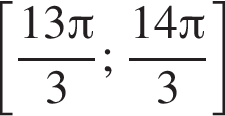
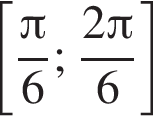
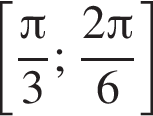
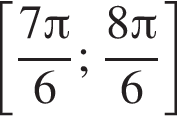
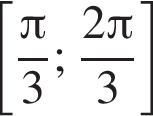
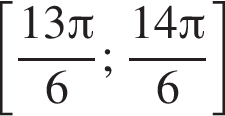
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
на которой выполнено неравенство. Также оно выполнено на всех сдвигах этой дуги на несколько оборотов, поэтому в указанном промежутке подходят отрезки 
31.
i
Дана система уравнений
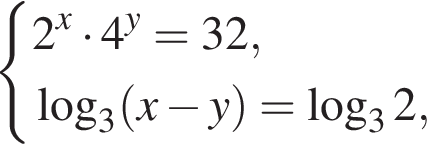
где (x; y) — решение данной системы. Сумма (x + y) принадлежит промежутку?
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
Домножая это уравнение на 2 и складывая с первым, получим 
откуда 
и 
следовательно, 
Ответ 3, 5 и 6.32.
i
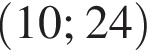
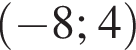
Найдите производную функции: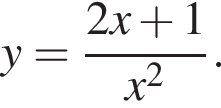 
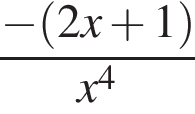
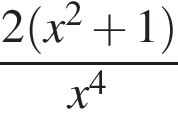
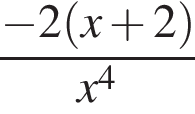
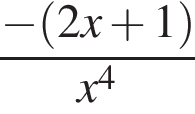
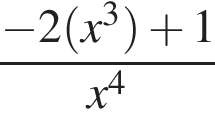
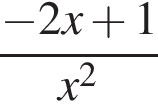
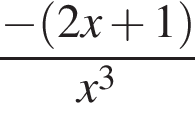
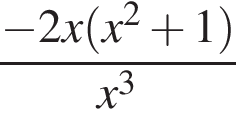
1) 
2) 
3) 
4)
5) 
6) 
7) 
8) 
33.
i
Даны векторы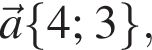 
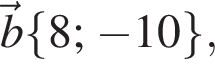
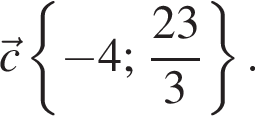Разложите вектор 
по векторам 
и 
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
тогда 
откуда
34.
i
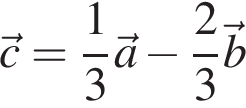
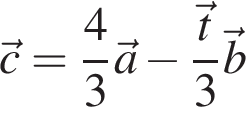
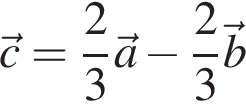
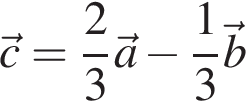
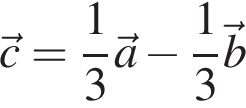
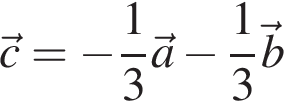
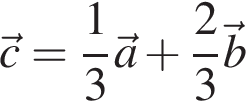
Укажите промежутки, в которых лежат экстремумы функции: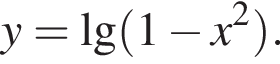 
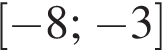
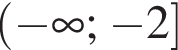
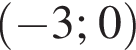
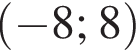
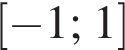
1) 
2) 
3) 
4)
5) 
6) 
7) 
8)
—
имеет экстремумы в тех же точках, что и сама функция 
которая возрастает при 
её график — парабола ветвями вниз с вершиной при 35.
i
В прямой правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 имеем 
и 
Найдите площадь боковой поверхности и площадь полной поверхности данной призмы.
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
следовательно, 
