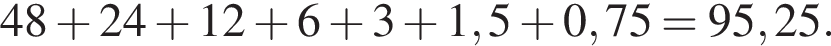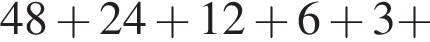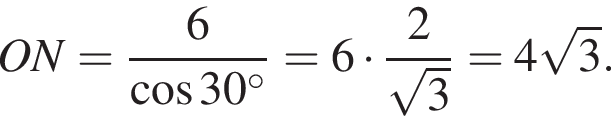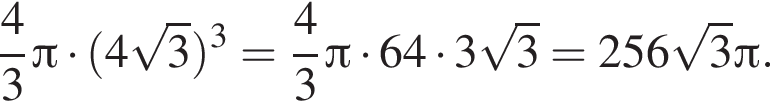1. Тип Д36 A36 № 2052 

Источник: Демонстрационная версия ЕНТ по математике 2022 года, вариант 1. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.12\. Вычисления и преобразования с модулем
Простые вопросы о числах, НОД и НОК, делители, доли, проценты. Задания для подготовки
i
Bыберите верные равенства:
1. 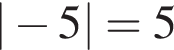
2. 
3. ![]()
4. 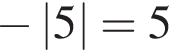
1) 3 и 4
2) 1 и 2
3) 2 и 4
4) 1 и 3
Решение. Заметим, что 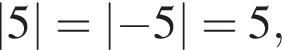 поэтому верны первое и третье равенства.
поэтому верны первое и третье равенства.
Правильный ответ указан под номером 4.
Ответ: 4
2052
4
Источник: Демонстрационная версия ЕНТ по математике 2022 года, вариант 1. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.12\. Вычисления и преобразования с модулем
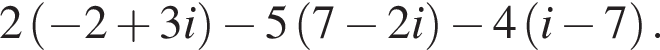
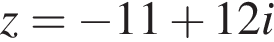
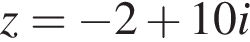
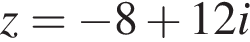
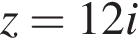
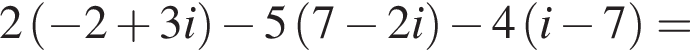
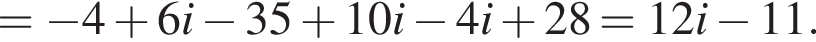

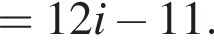
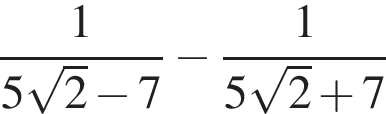 кратно?
кратно?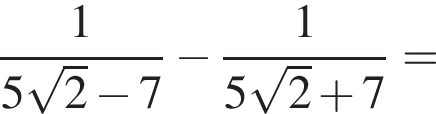
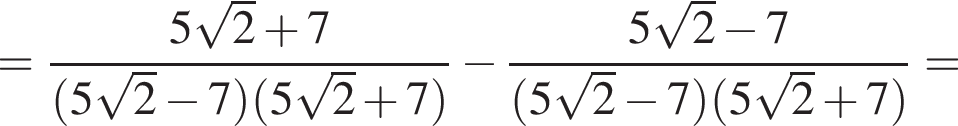
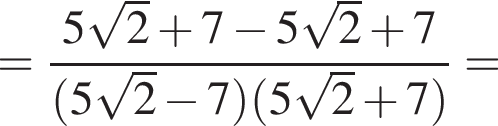
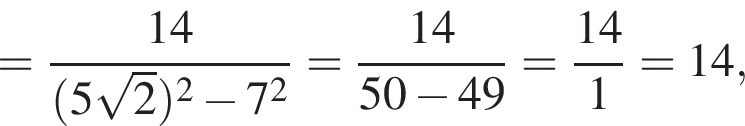
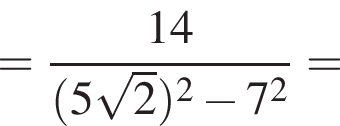
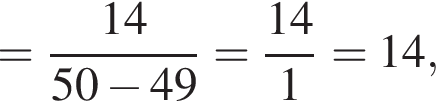
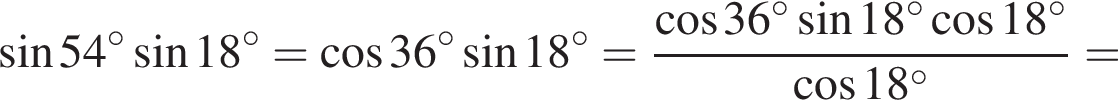
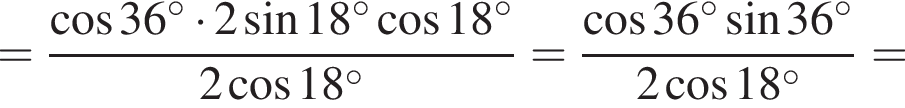
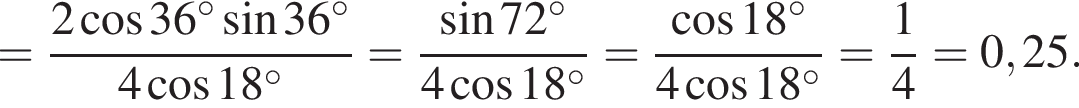
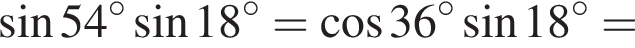
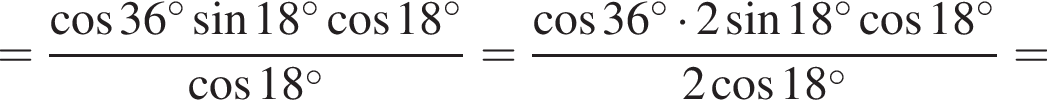
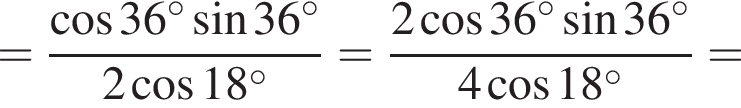
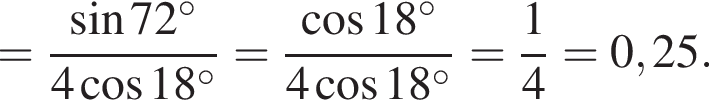
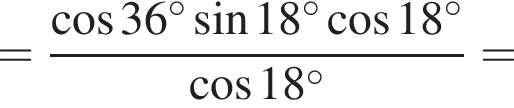
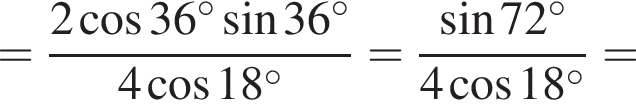
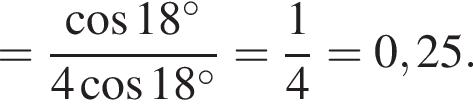
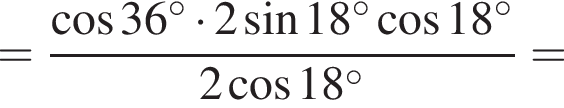
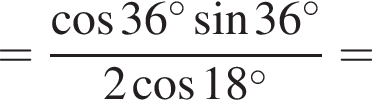


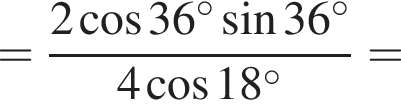
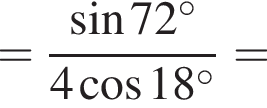
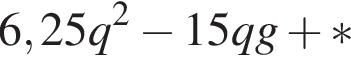 можно было представить в виде квадрата двучлена
можно было представить в виде квадрата двучлена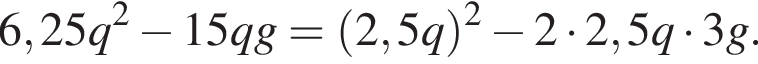
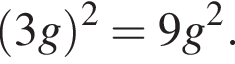
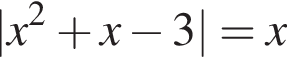 имеет иррациональный корень
имеет иррациональный корень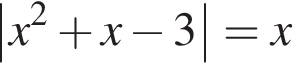 возможно только при неотрицательных x. Рассмотрим два случая.
возможно только при неотрицательных x. Рассмотрим два случая.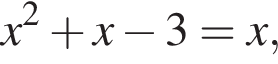 то
то  откуда
откуда  Нам подходит только корень
Нам подходит только корень  он иррационален.
он иррационален.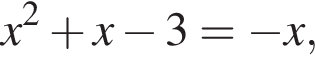 то есть
то есть 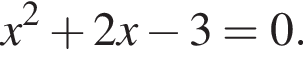 Это квадратное уравнение имеет корни
Это квадратное уравнение имеет корни 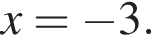 Второй посторонний, а первый рациональный.
Второй посторонний, а первый рациональный. где (x; y) — решение системы уравнений
где (x; y) — решение системы уравнений  причем y < 0.
причем y < 0.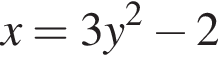 и подставить это выражение в первое уравнение. Получим
и подставить это выражение в первое уравнение. Получим 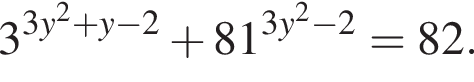
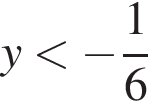 оба показателя степени убывают, поэтому оба слагаемых и их сумма убывают. Значит, на промежутке
оба показателя степени убывают, поэтому оба слагаемых и их сумма убывают. Значит, на промежутке 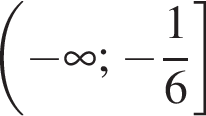 может быть не более одного корня. Подбором находим, что
может быть не более одного корня. Подбором находим, что 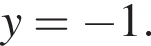 Тогда
Тогда 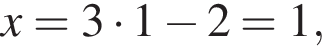 а искомая сумма
а искомая сумма 
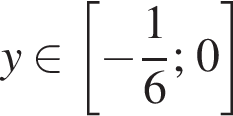 оба показателя степени отрицательны, поэтому сумма двух слагаемых не превосходит
оба показателя степени отрицательны, поэтому сумма двух слагаемых не превосходит 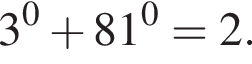 На этом промежутке нет корней. Положительные значения y исследовать не нужно, так как по условию y < 0.
На этом промежутке нет корней. Положительные значения y исследовать не нужно, так как по условию y < 0.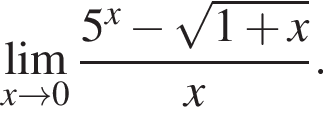
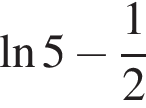
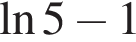
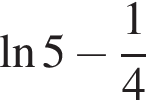
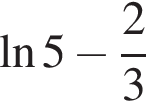
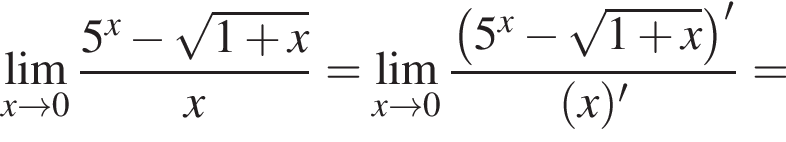
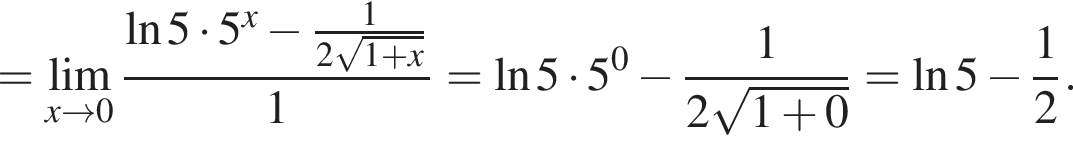
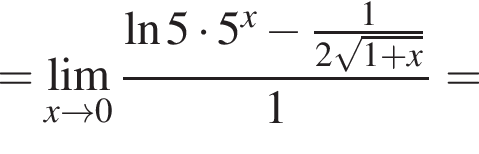
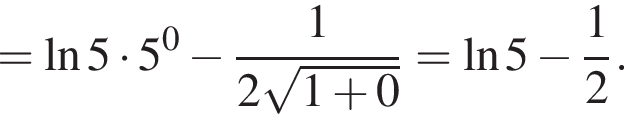
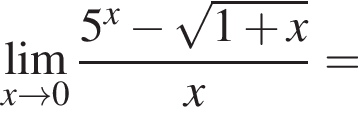

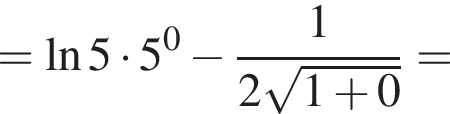
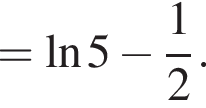
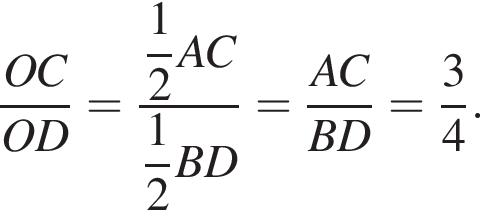
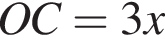 и
и  тогда по теореме Пифагора для треугольника OCD получаем
тогда по теореме Пифагора для треугольника OCD получаем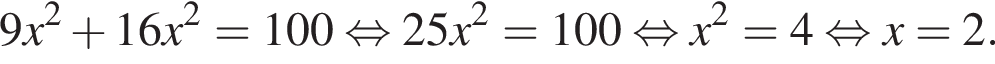

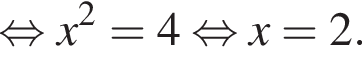


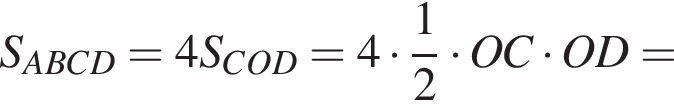
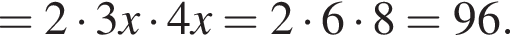

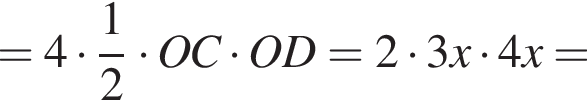
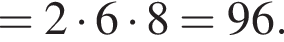

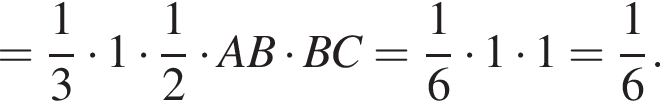
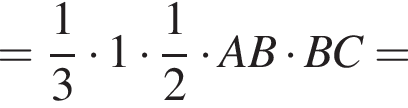
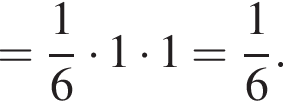
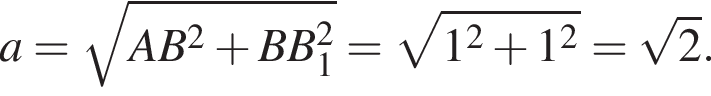
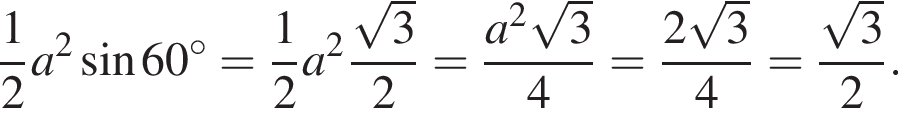
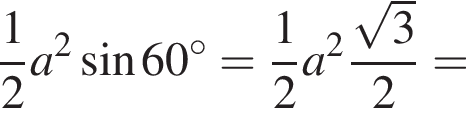
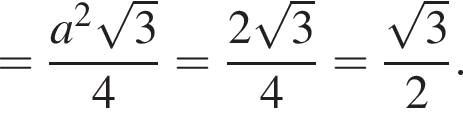
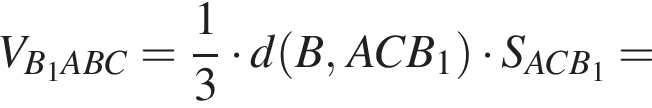
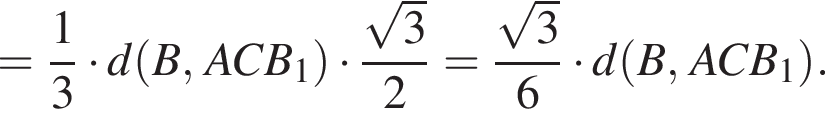
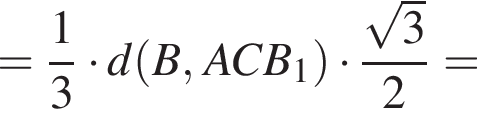
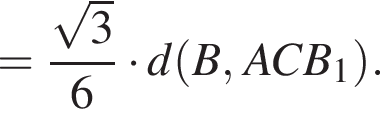
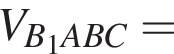
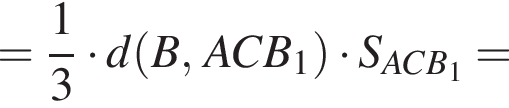
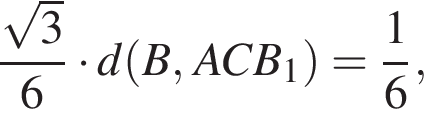 откуда
откуда 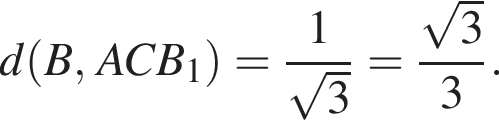
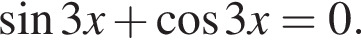
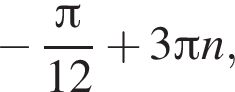
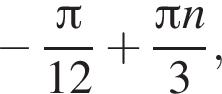
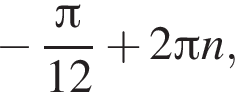
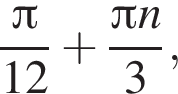
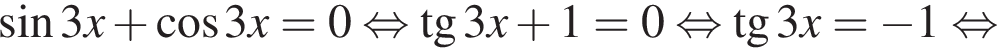
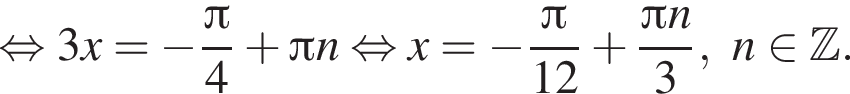
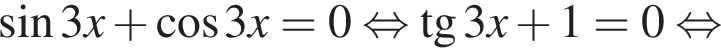
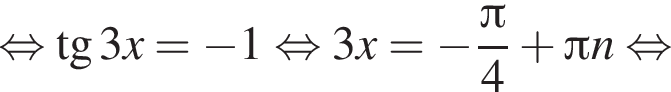
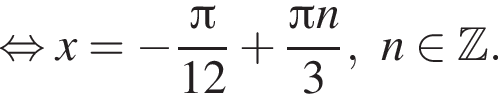

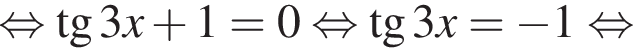
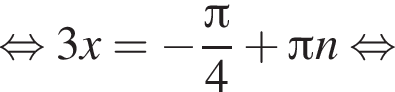

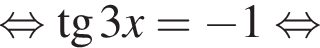
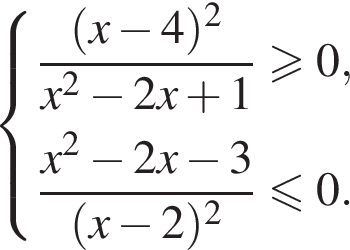
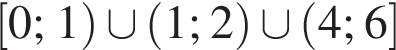
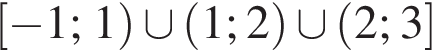
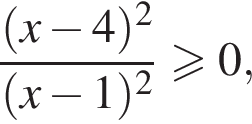
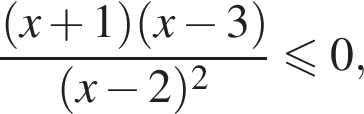
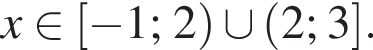 Значит, ответом на систему будет
Значит, ответом на систему будет 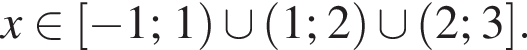
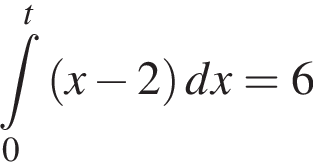 равен?
равен?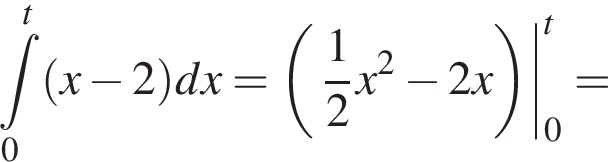
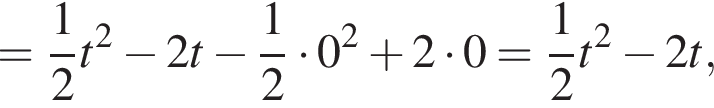

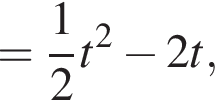
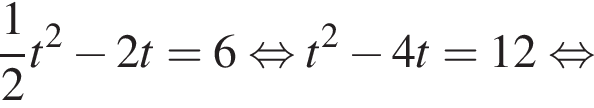

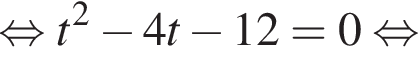
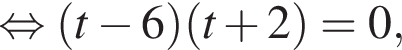
 или
или 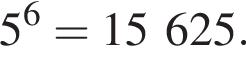 Итак, количество нужных нам чисел равно
Итак, количество нужных нам чисел равно 
 если известно, что угол
если известно, что угол 
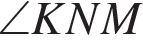 —
—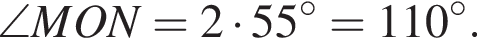
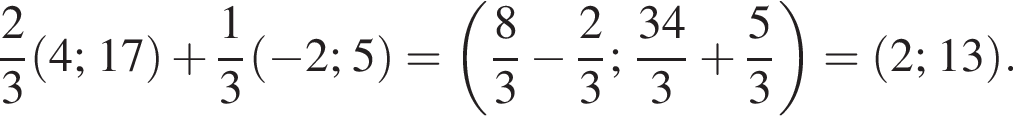
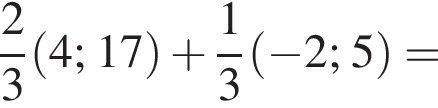
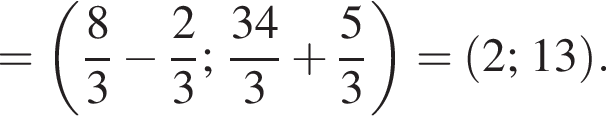
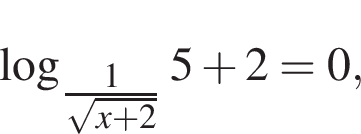 в ответе запишите произведение корней или корень, если он единственный.
в ответе запишите произведение корней или корень, если он единственный.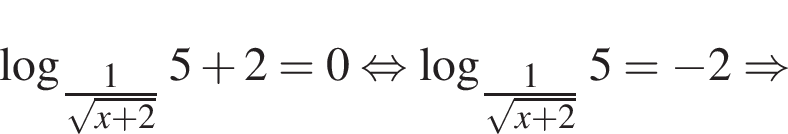
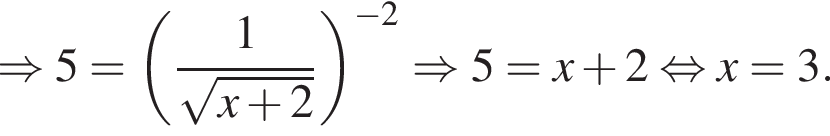
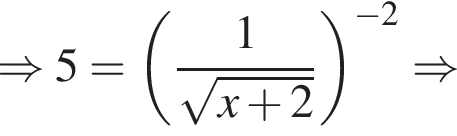

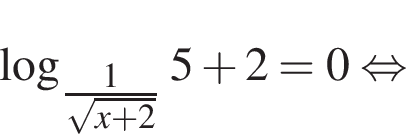
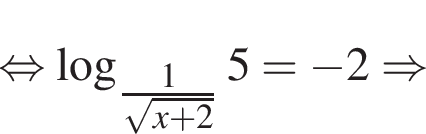
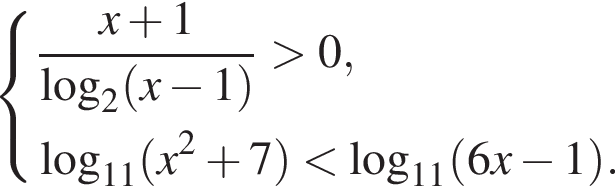


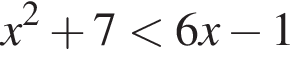 (поскольку
(поскольку 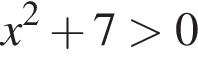 при всех x), то есть
при всех x), то есть 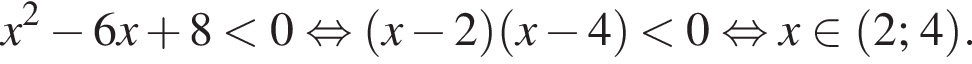
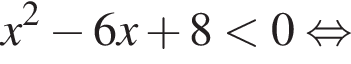

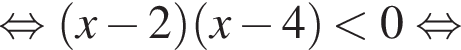

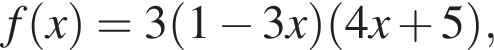 проходящую через точку
проходящую через точку 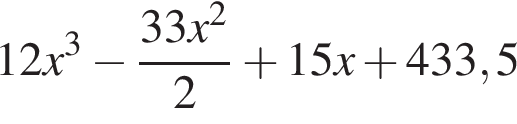
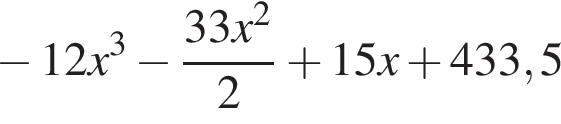
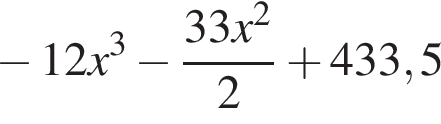
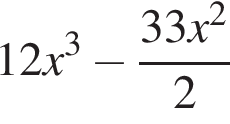
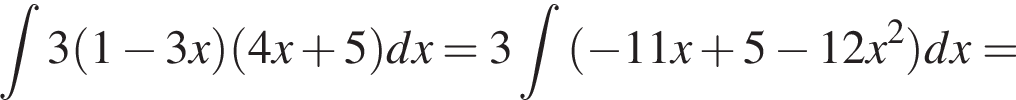
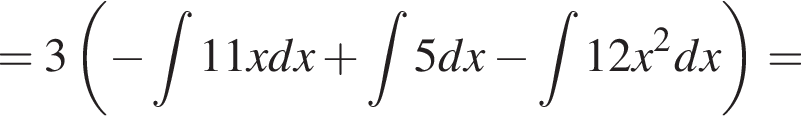
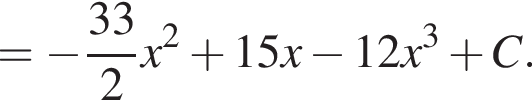
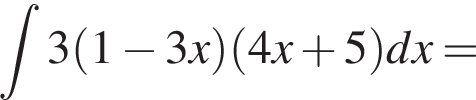
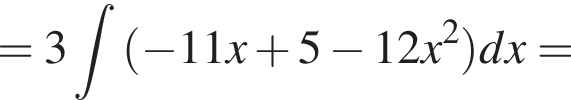
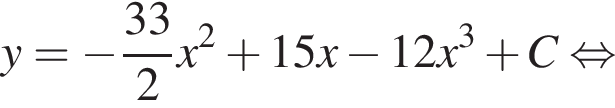
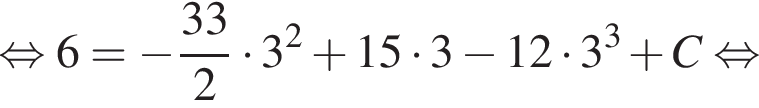
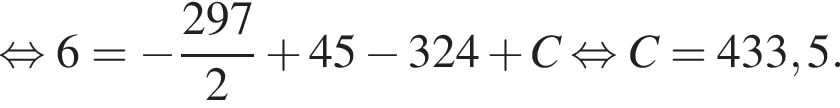
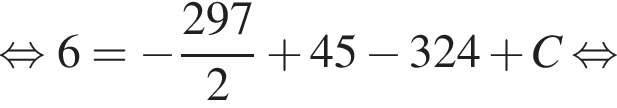
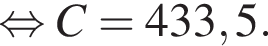
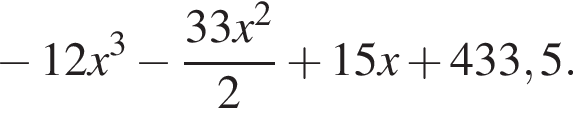
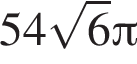
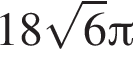
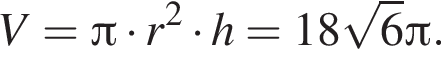
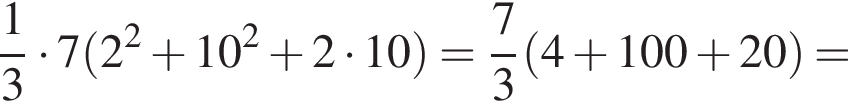
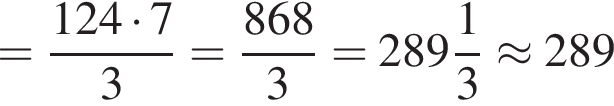
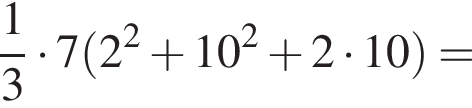
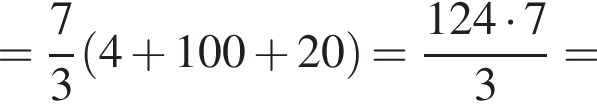
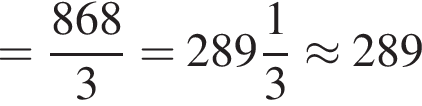
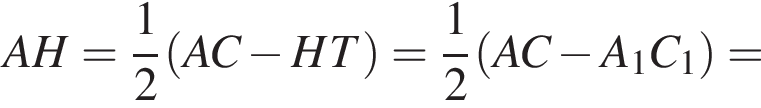
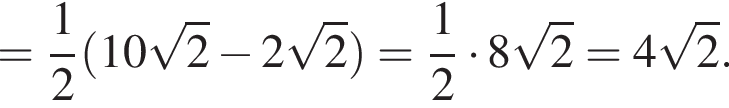
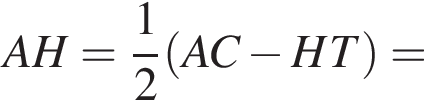
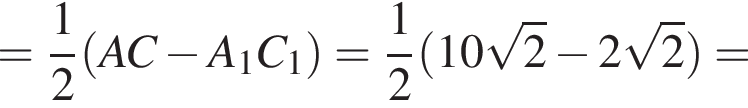
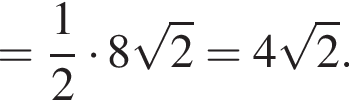
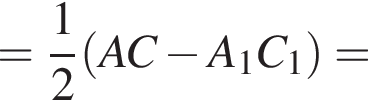
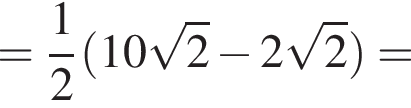
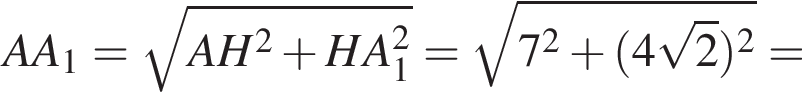


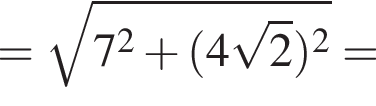
 метров
метров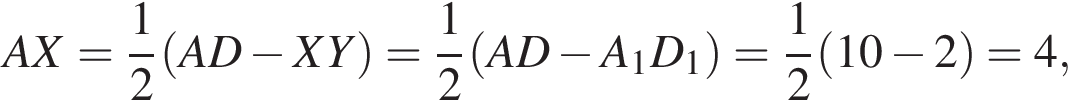
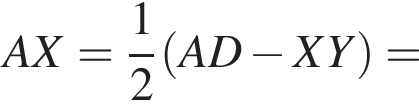
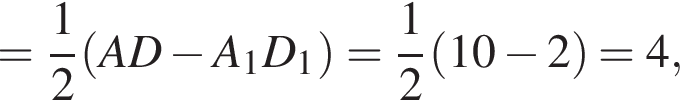

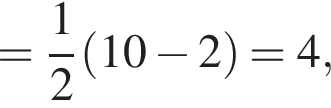
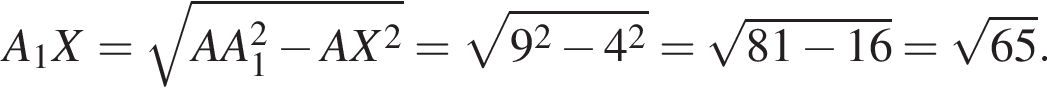
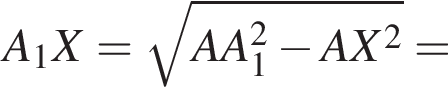
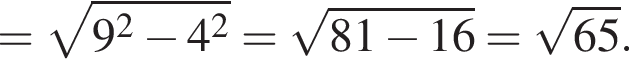
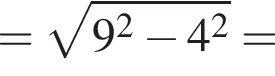

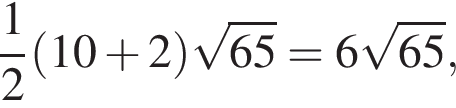
 поэтому расход штукатурки составит
поэтому расход штукатурки составит 

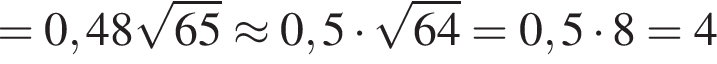
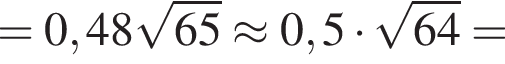


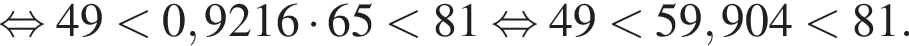


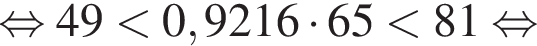
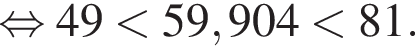
 грамм на кубический метр или 2500 кг на кубометр. Значит, масса постамента составит
грамм на кубический метр или 2500 кг на кубометр. Значит, масса постамента составит 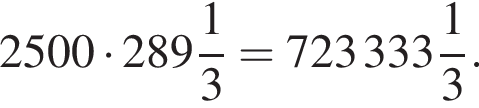
 Первое неравенство очевидно. Второе же равносильно
Первое неравенство очевидно. Второе же равносильно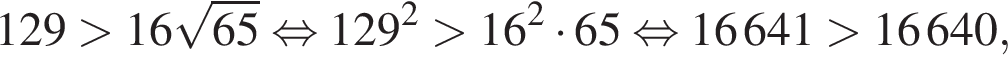
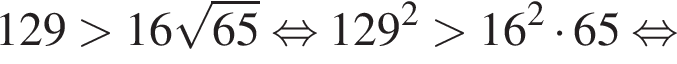
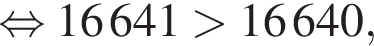
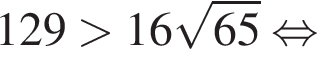

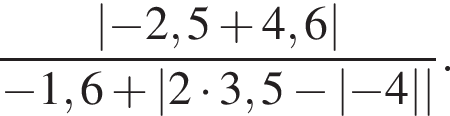
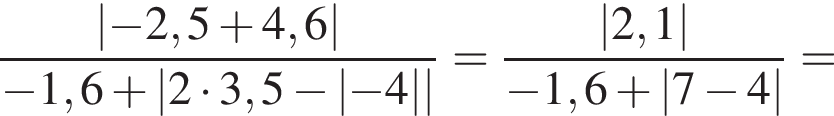
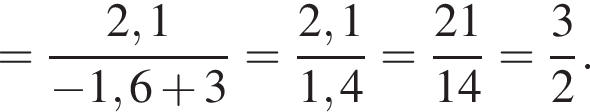
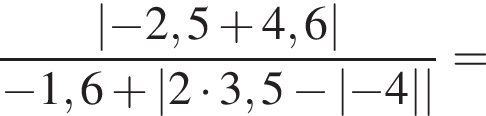
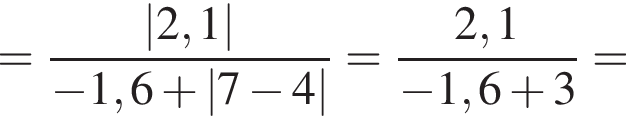
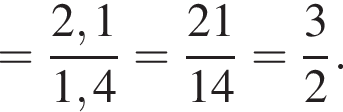
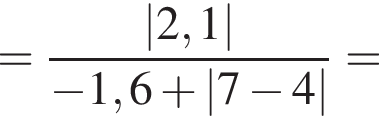
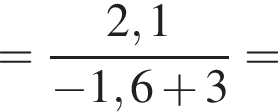
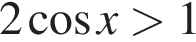 .
.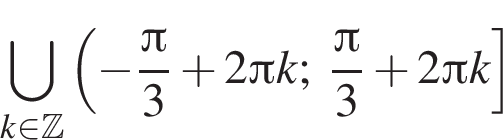
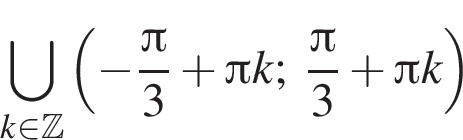
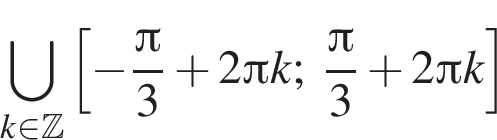
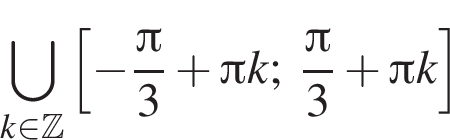
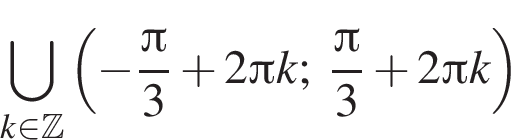
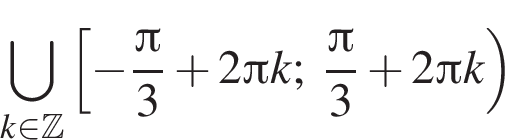
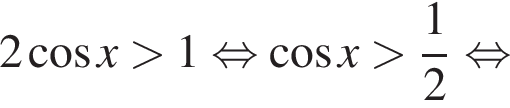
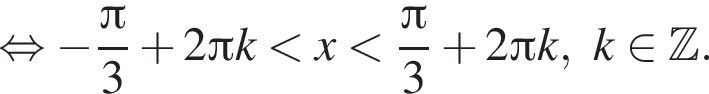
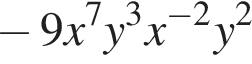
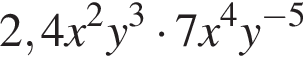
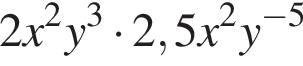
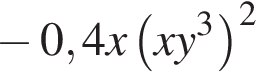
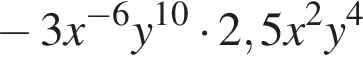
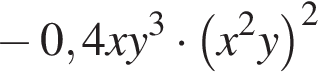
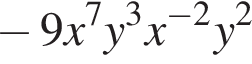 получаем
получаем 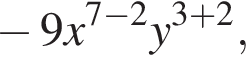 то есть
то есть 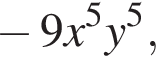 где степень равна
где степень равна 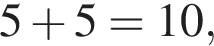 подходит;
подходит;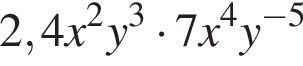 получаем
получаем 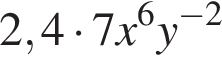 —
—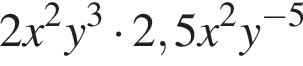 получаем
получаем 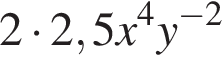 —
—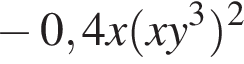 получаем
получаем 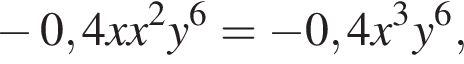 где степень равна
где степень равна  не подходит;
не подходит;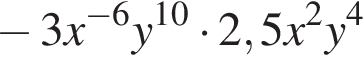 получаем
получаем 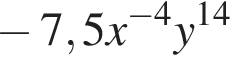 —
—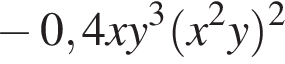 получаем
получаем 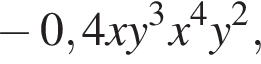 то есть
то есть 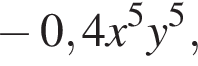 степень равна
степень равна 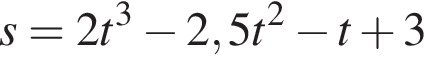 (s — в метрах, t — в секундах). В какой момент времени скорость точки равна нулю.
(s — в метрах, t — в секундах). В какой момент времени скорость точки равна нулю.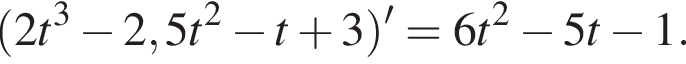
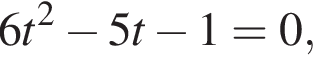 получаем
получаем 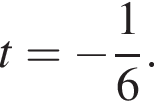 Обычно за
Обычно за  и
и  поэтому координатами F будут
поэтому координатами F будут 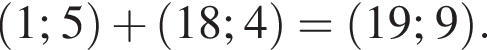
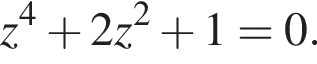
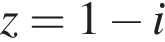
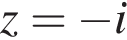
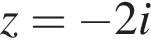
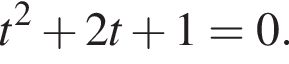 Пусть
Пусть 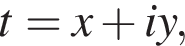 где x и y — вещественные числа. Тогда:
где x и y — вещественные числа. Тогда: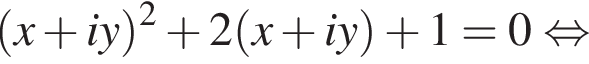

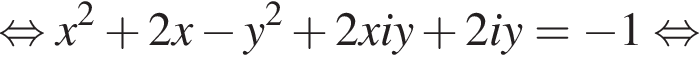
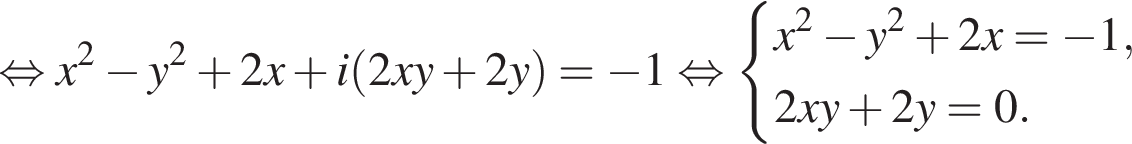
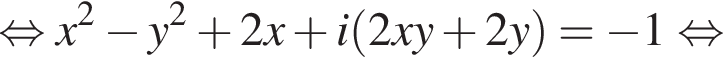
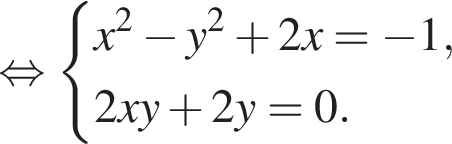
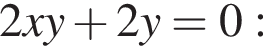
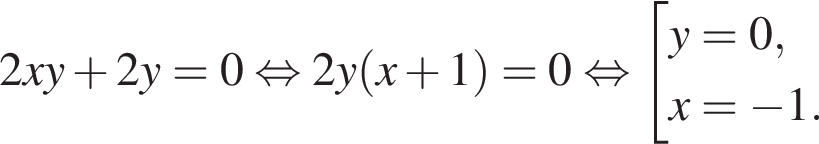
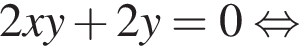


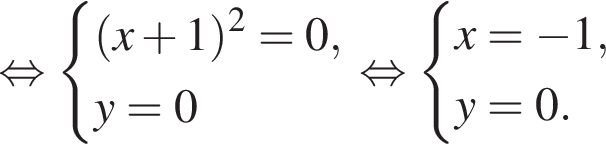
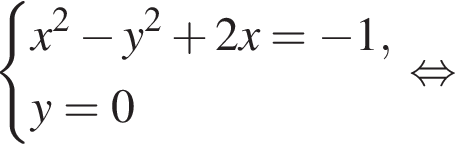
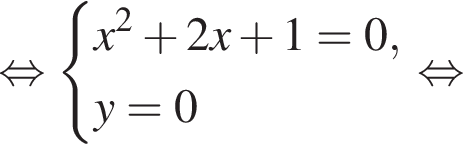
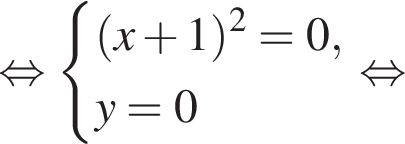
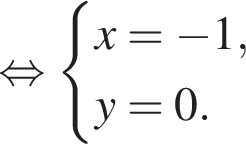

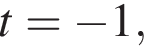 тогда
тогда 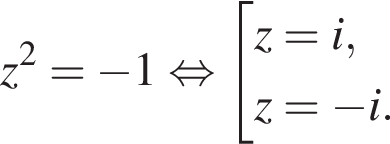
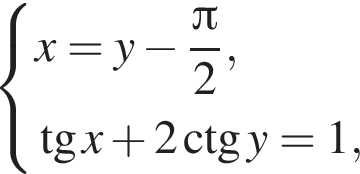 если
если 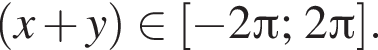
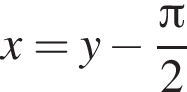 во второе уравнение, получаем
во второе уравнение, получаем 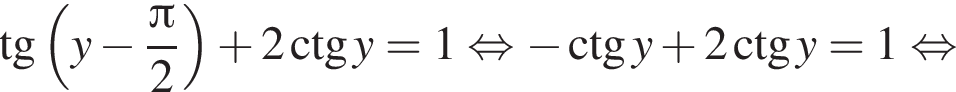
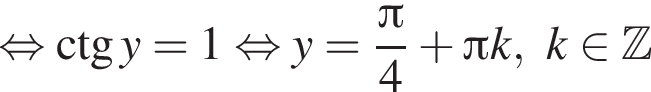
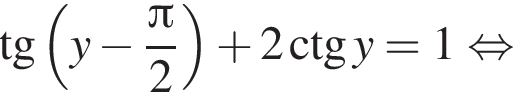
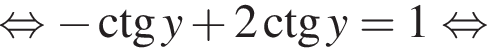

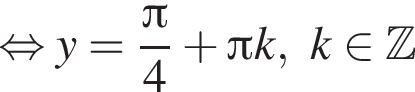
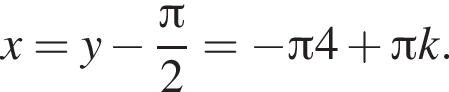 Тогда
Тогда 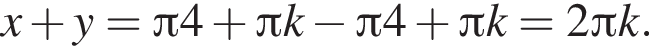
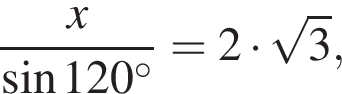
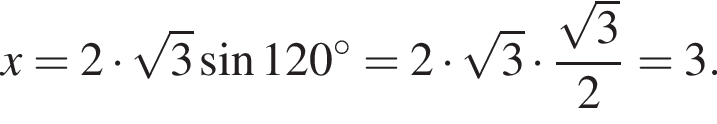
 раза меньше предыдущего. Вычислим их и посчитаем сумму:
раза меньше предыдущего. Вычислим их и посчитаем сумму: