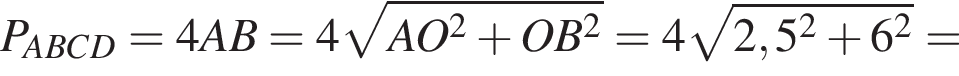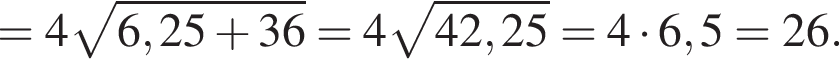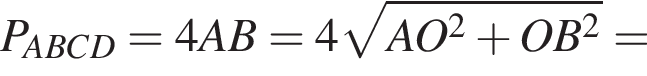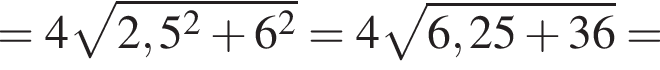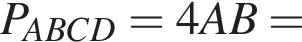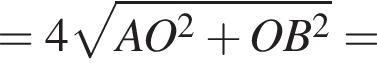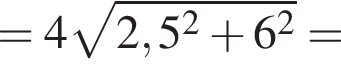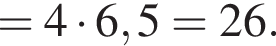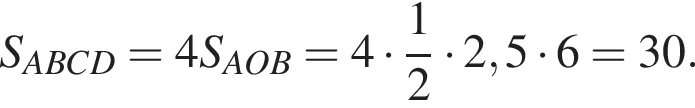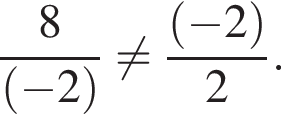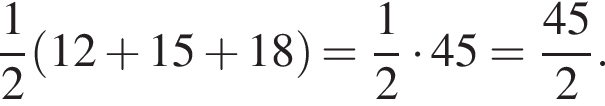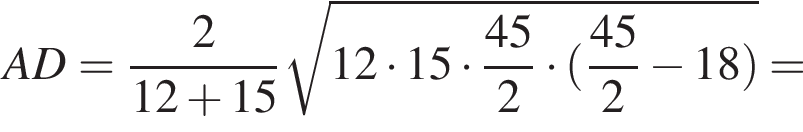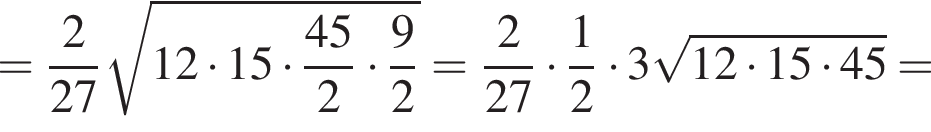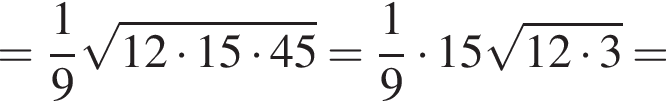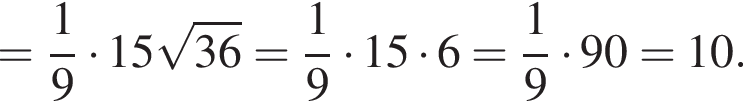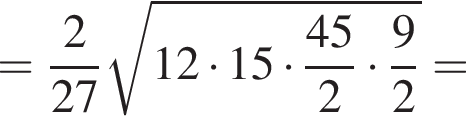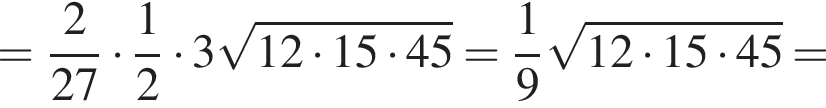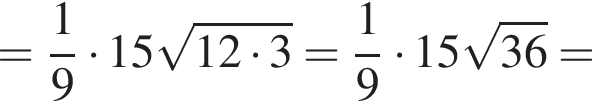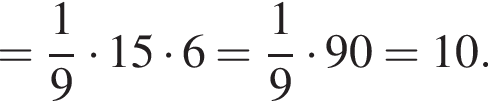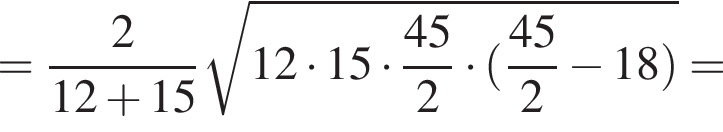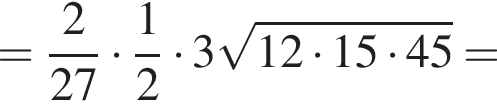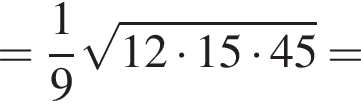Одно число меньше другого на 42, что составляет 14% большего числа. Найдите меньшее число.
Вычислите: 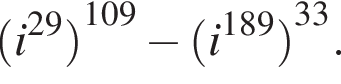
Вычислите 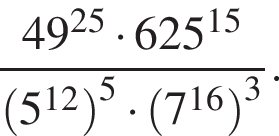
Найдите значение выражения 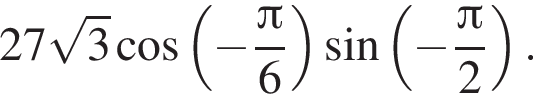
Значение выражения 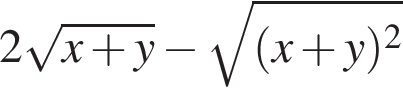 при
при  равно
равно
Числитель дроби на 4 меньше ее знаменателя. Если эту дробь сложить с обратной ей дробью, то получится число ![]() Найдите исходную дробь.
Найдите исходную дробь.
Найдите число А, если 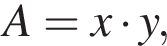 где (x; y) является решением системы уравнений
где (x; y) является решением системы уравнений 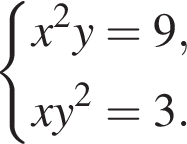
Найдите предел в точке 
Катеты прямоугольного треугольника равны 10 и 24. Высота, проведённая к гипотенузе, равна
Найдите угол между плоскостями, если
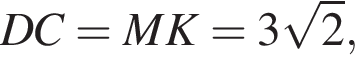
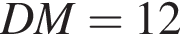 см
см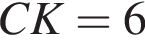 см.
см.
Решите уравнение: 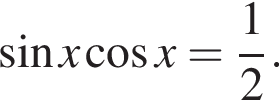


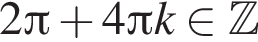
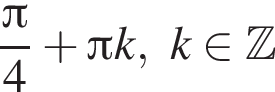
Решите систему неравенств: Not match begin/end
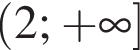
Вычислите 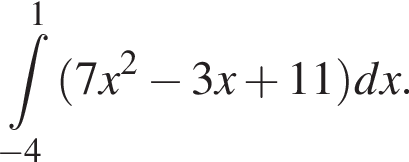
Сколькими способами можно усадить 7 человек за круглый стол?
В окружности с центром в точке O построены параллельные хорды AB и ED. Угол ECD равен 60°,
 Длина хорды ED равна
Длина хорды ED равна
Найдите расстояние от точки A (1; −2; 3) до координатной прямой Oy
Найдите сумму корней (корень, если он единственный) уравнения 
Решите систему неравенств: 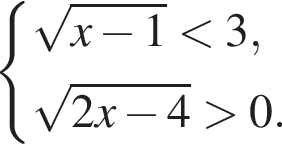
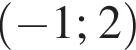
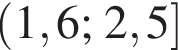
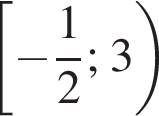
Найдите неопределённый интеграл 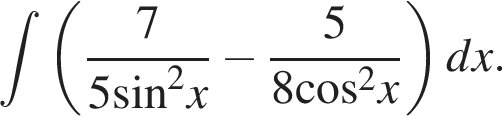
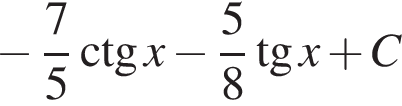
Усеченный конус, у которого радиусы оснований равны 7 и 8, и полный конус такой же высоты равновелики. Найдите радиус основания полного конуса.
В крестьянском хозяйстве взвесили клубни картофеля. Массы клубней (в граммах) приведены в таблице.
| 60 | 59 |
| 57 | 59 |
| 56 | 58 |
| 61 | 61 |
| 58 | 59 |
Определите объем выборки.
В крестьянском хозяйстве взвесили клубни картофеля. Массы клубней (в граммах) приведены в таблице.
| 60 | 59 |
| 57 | 59 |
| 56 | 58 |
| 61 | 61 |
| 58 | 59 |
Найдите моду вариационного ряда.
В крестьянском хозяйстве взвесили клубни картофеля. Массы клубней (в граммах) приведены в таблице.
| 60 | 59 |
| 57 | 59 |
| 56 | 58 |
| 61 | 61 |
| 58 | 59 |
Разность между самым легким и тяжелым клубнем равна
В крестьянском хозяйстве взвесили клубни картофеля. Массы клубней (в граммах) приведены в таблице.
| 60 | 59 |
| 57 | 59 |
| 56 | 58 |
| 61 | 61 |
| 58 | 59 |
Найдите среднюю массу клубня картофеля.
В крестьянском хозяйстве взвесили клубни картофеля. Массы клубней (в граммах) приведены в таблице.
| 60 | 59 |
| 57 | 59 |
| 56 | 58 |
| 61 | 61 |
| 58 | 59 |
Для данной выборки определите математическое ожидание массы клубня. Ответ округлите до целых.
Вычислите 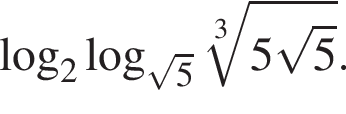
Решите однородное уравнение первой степени 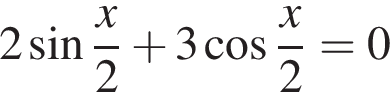 .
.
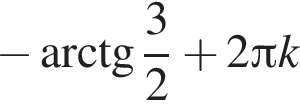
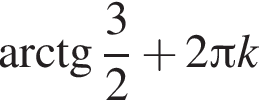
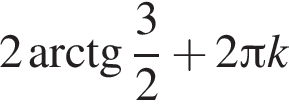
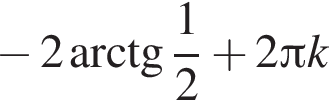
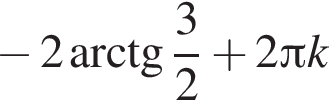
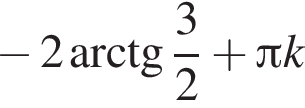
Результат упрощения выражения 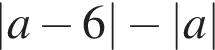 при
при 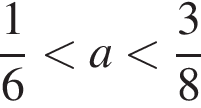 имеет вид:
имеет вид:
Hайдите наименьшее значение функции: 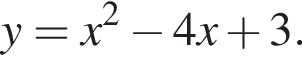
Найдите координаты вектора ![]() если
если 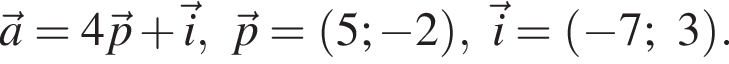
Упростите выражение: 



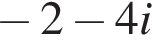
Корнями уравнения 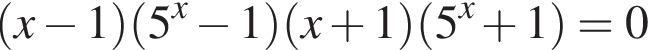 являются
являются
Найдите периметр и площадь ромба, если его диагонали равны 5 см и 1,2 дм.
Определите, какая из предложенных последовательностей не является геометрической прогрессией.
Дан треугольник АВС, у которого АВ = 15 м, ВС = 18 м и АС = 12 м. Найдите длину биссектрисы АD.

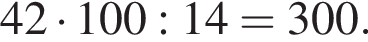 Таким образом, меньшее число
Таким образом, меньшее число 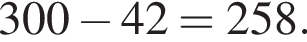
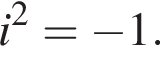
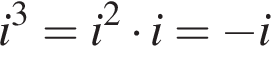 и
и 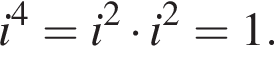 Тогда
Тогда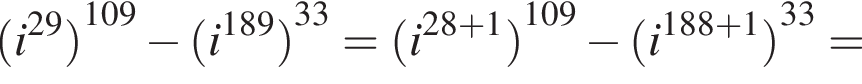
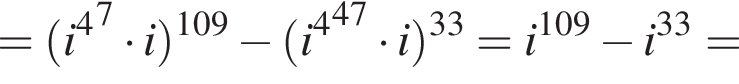
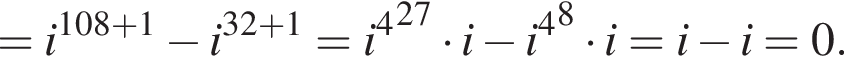
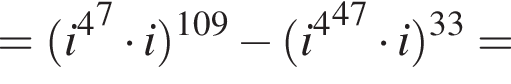
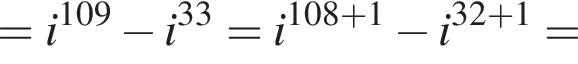
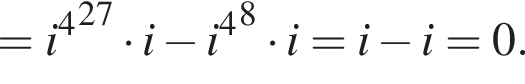
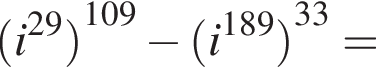

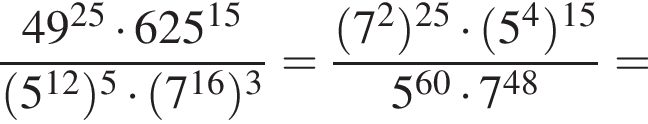
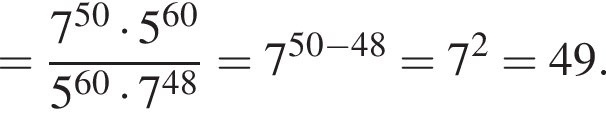
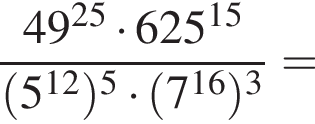
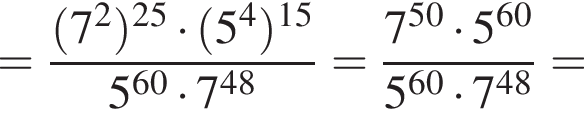
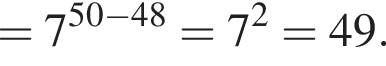
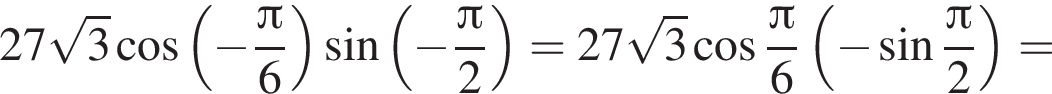
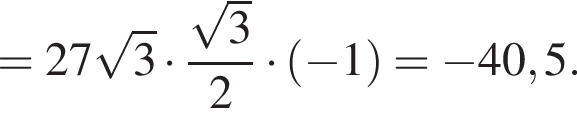
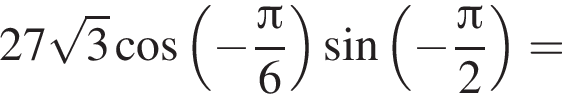
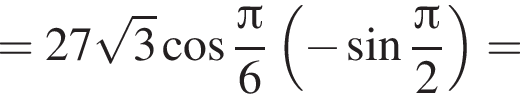
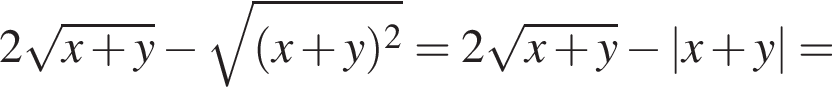
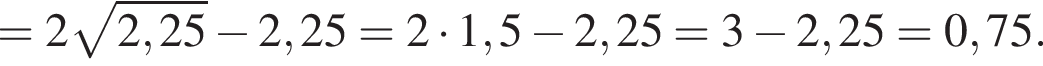
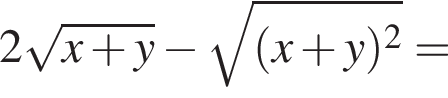
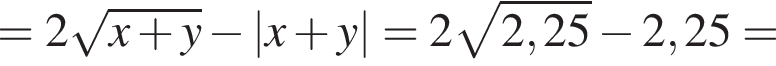

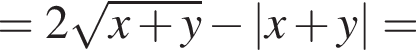
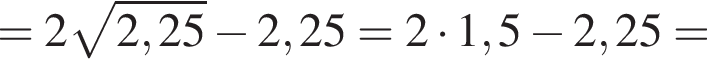

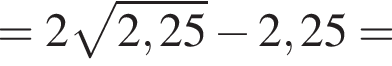

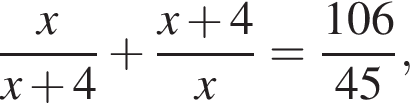
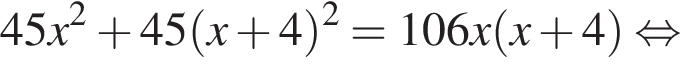
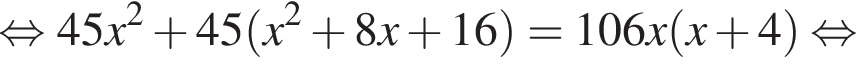
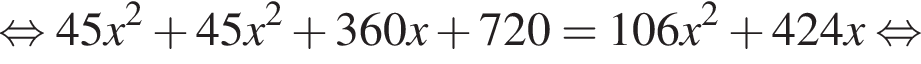
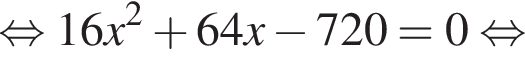

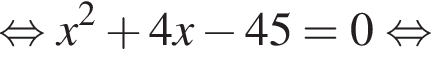
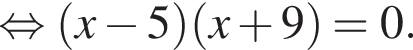
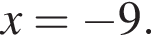 Видимо имеется в виду, что дробь равна
Видимо имеется в виду, что дробь равна 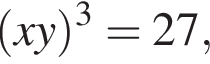 откуда
откуда 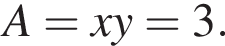

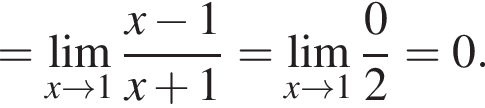
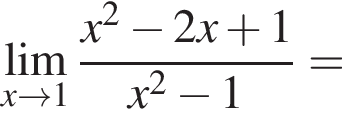

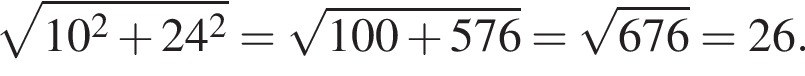


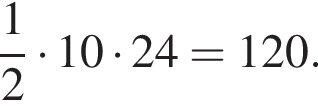 Значит, высота, проведенная к гипотенузе, равна
Значит, высота, проведенная к гипотенузе, равна 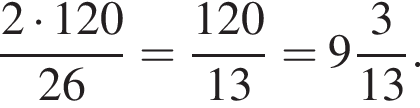
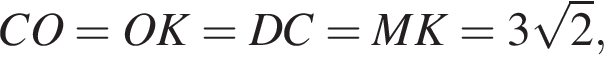

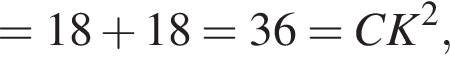
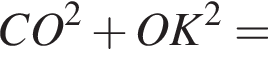

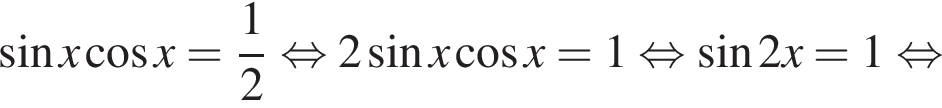
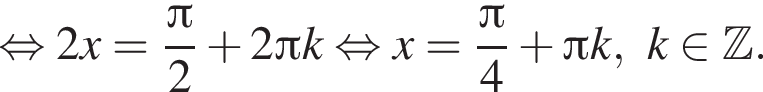
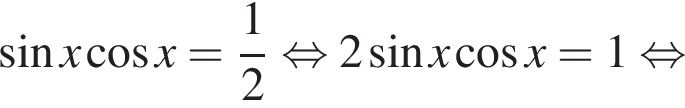
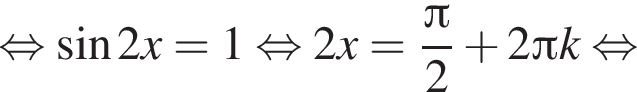
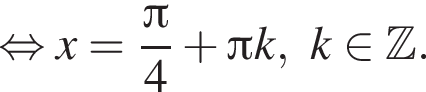
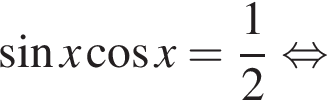
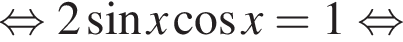
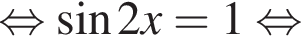
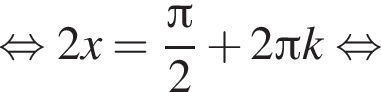
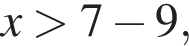 откуда
откуда 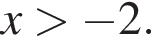 Второе — к
Второе — к 

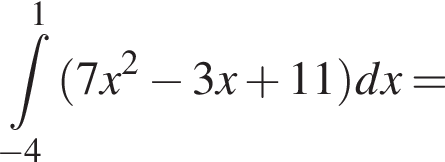
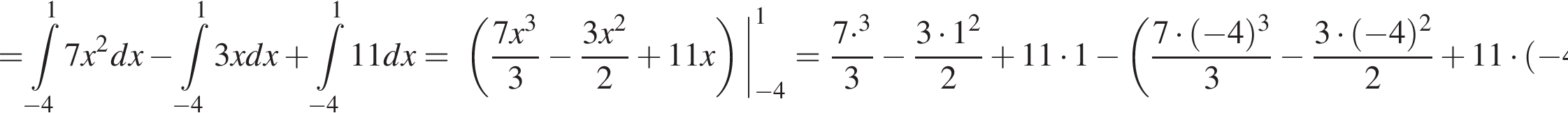
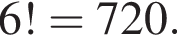

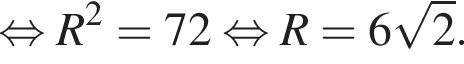
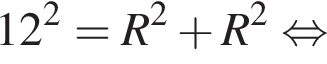

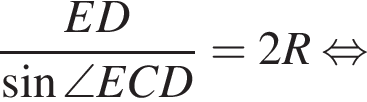
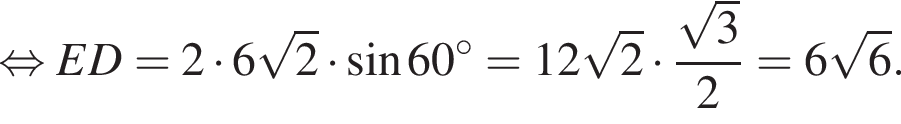
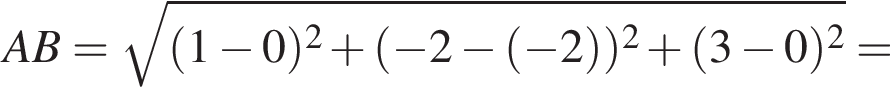
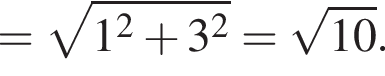
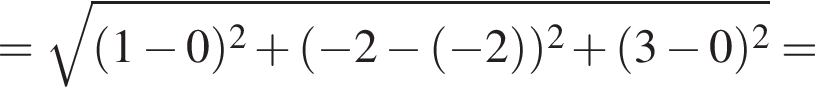
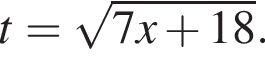 Тогда:
Тогда: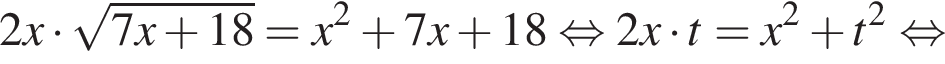

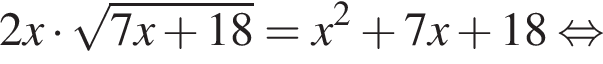


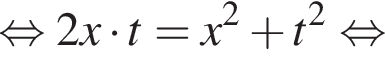
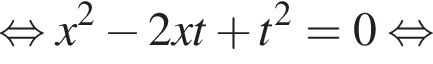
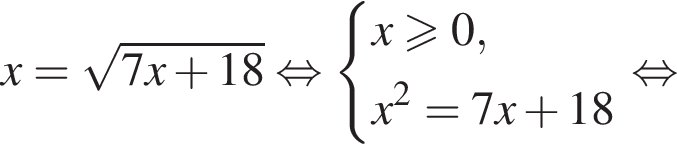
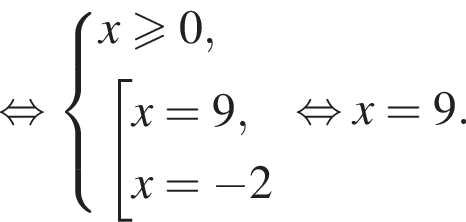
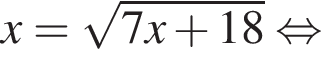
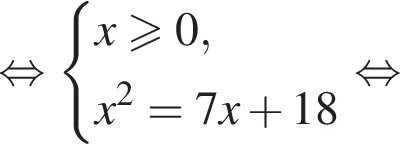

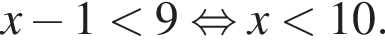
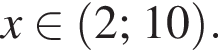
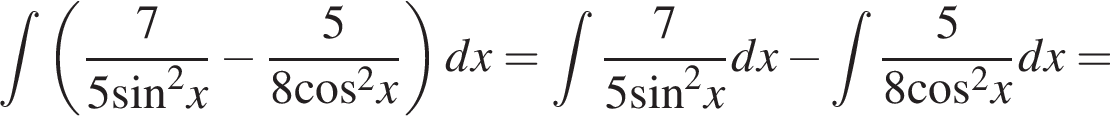
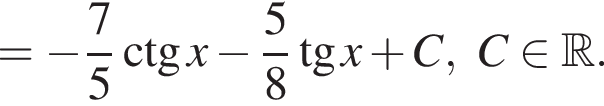
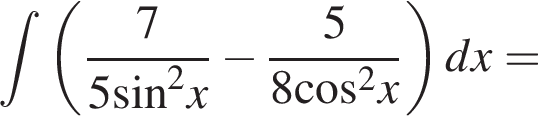
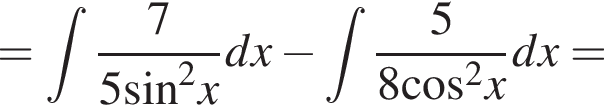
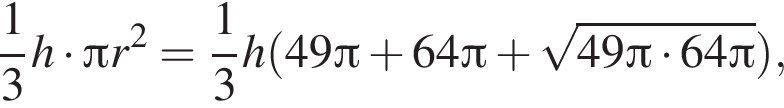
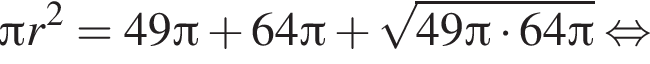
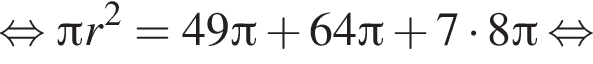


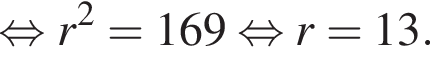
 граммов.
граммов.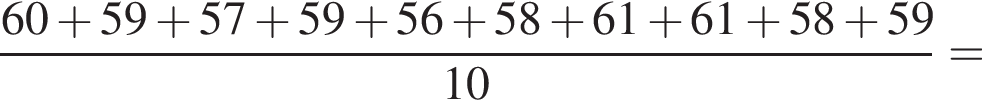
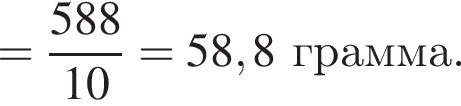

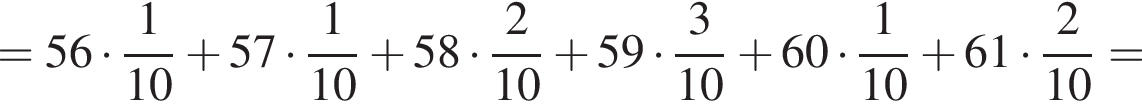
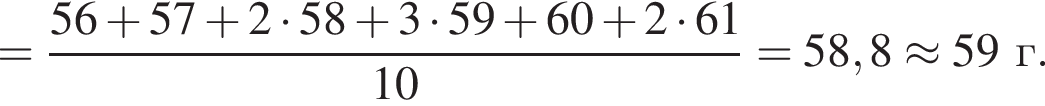
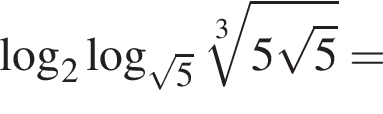
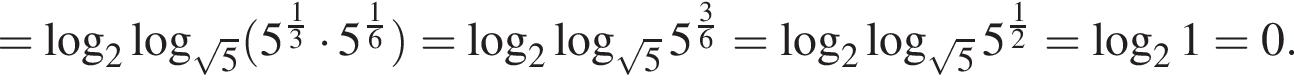
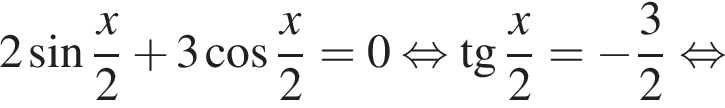
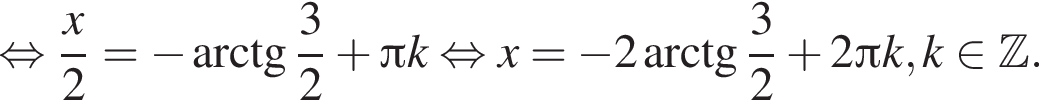
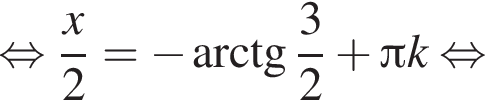
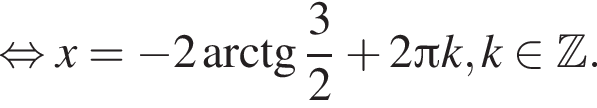
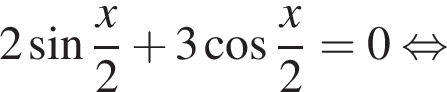
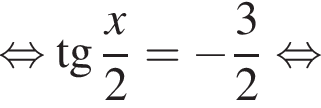


 и рассмотрим систему
и рассмотрим систему 

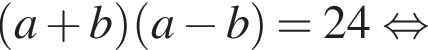
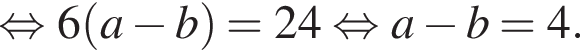
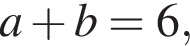 получаем
получаем  откуда
откуда 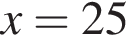 и
и 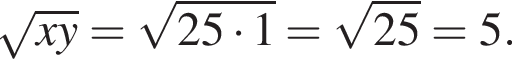 Это число дано в ответах 1, 6 и 8, просто по-разному записано.
Это число дано в ответах 1, 6 и 8, просто по-разному записано. 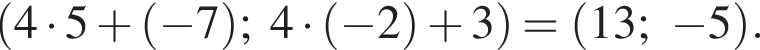
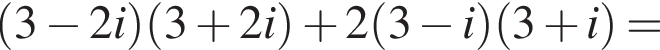
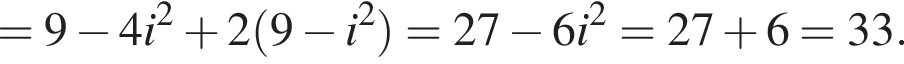
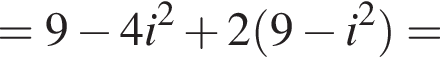

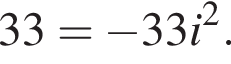
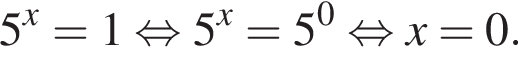
 и
и  сантиметров. Тогда во-первых
сантиметров. Тогда во-первых