1. Тип 1 № 1937 

Классификатор алгебры: 1\.1\. Действия с числами, степенями, дробями
Числовые алгебраические выражения. Задания для подготовки
i
Найдите значение выражения 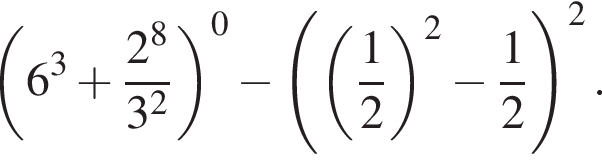
1) 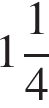
2) 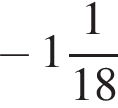
3) 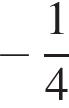
4) 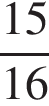
Решение. Найдем значение выражения:
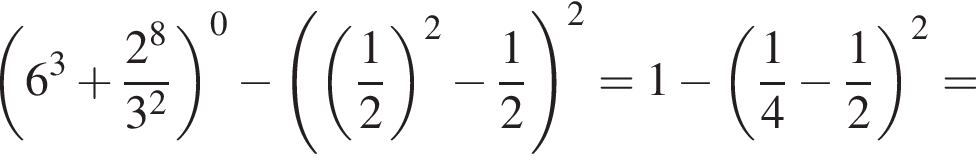
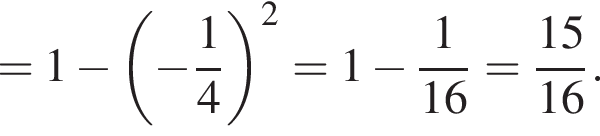
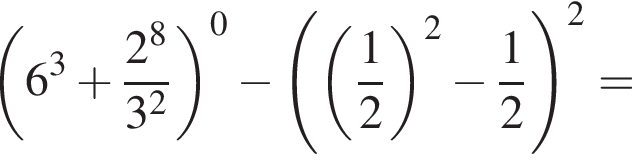
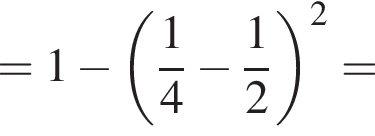
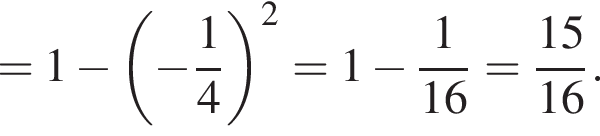
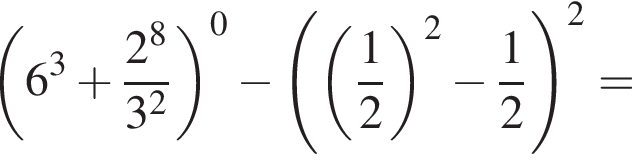
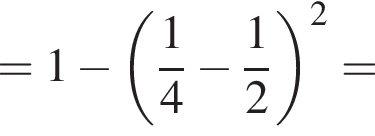
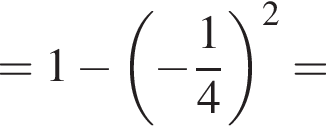
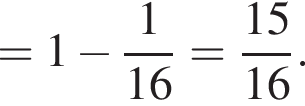
Правильный ответ указан под номером 4.
Ответ: 4
1937
4
Классификатор алгебры: 1\.1\. Действия с числами, степенями, дробями
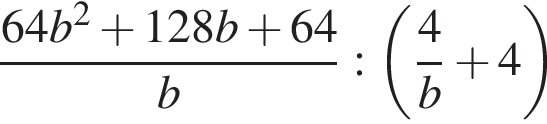 при
при 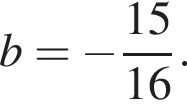
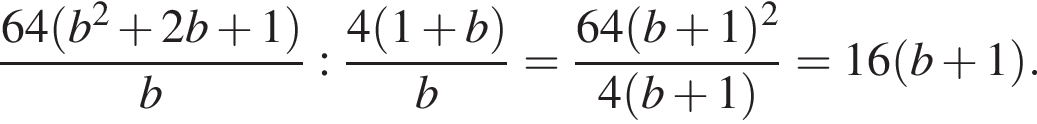
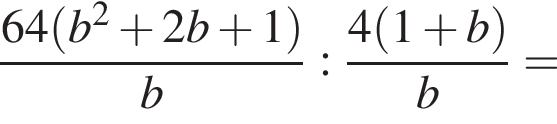
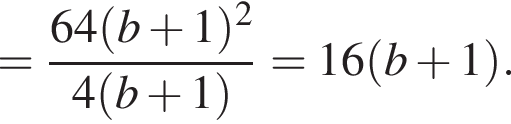
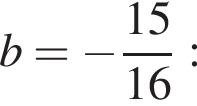
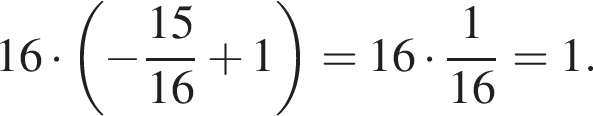
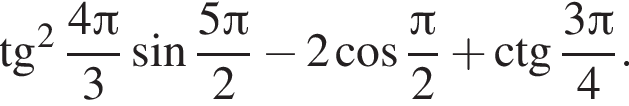
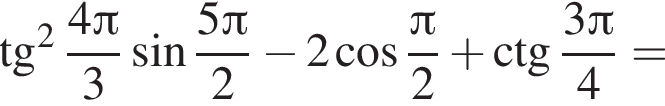
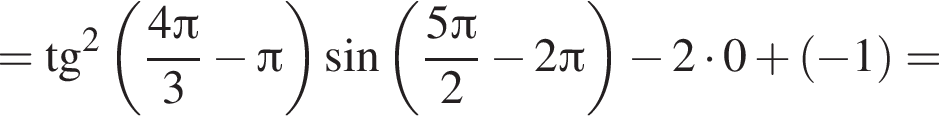
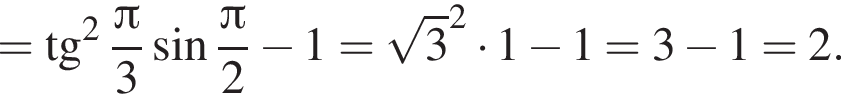

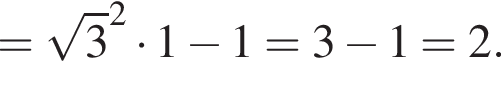
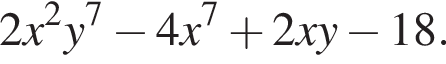
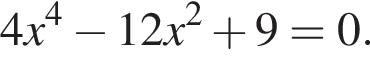

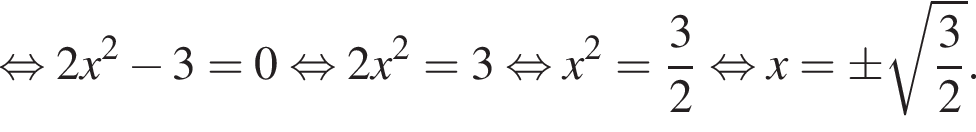
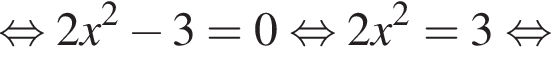
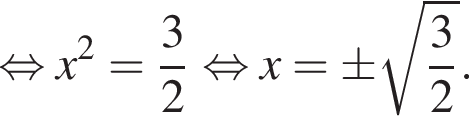
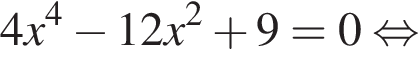
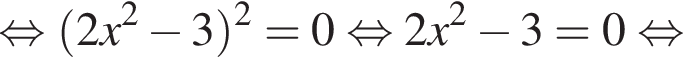

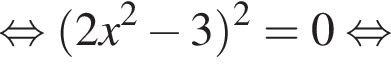
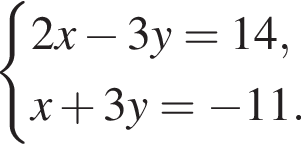
 откуда
откуда 
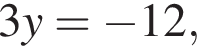
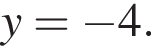 Значит,
Значит, 
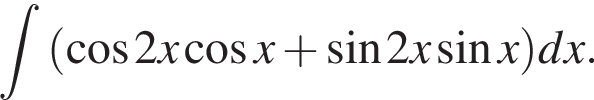
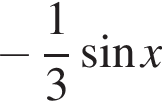
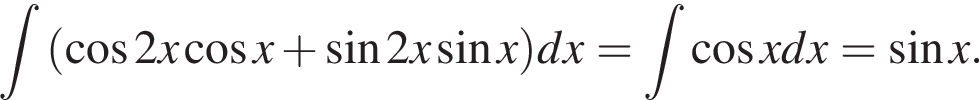
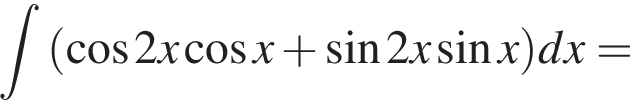
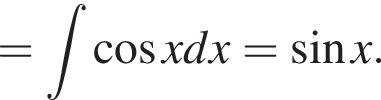
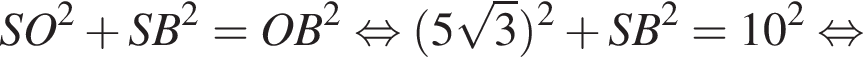
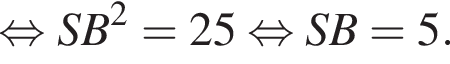
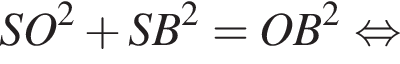
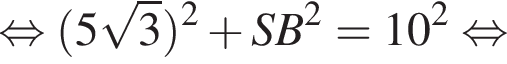
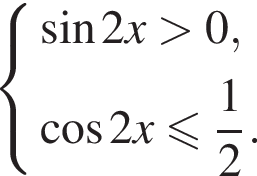
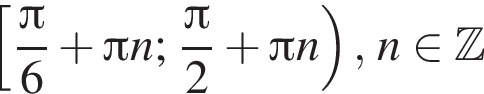
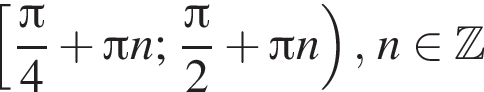
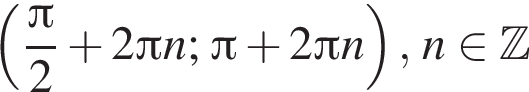
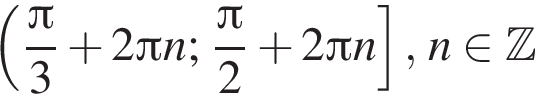
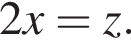 На единичной окружности (см. рисунок) отметим дуги, на которых
На единичной окружности (см. рисунок) отметим дуги, на которых 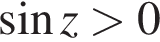 и
и 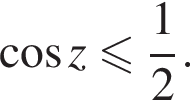 Пересечением этих дуг будет дуга
Пересечением этих дуг будет дуга 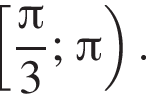 Значит,
Значит, 
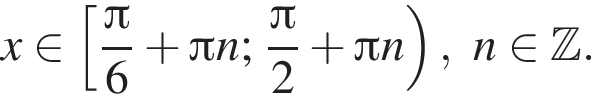
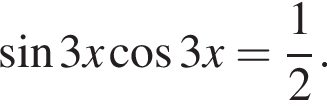
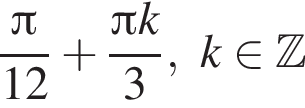
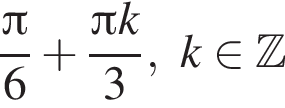
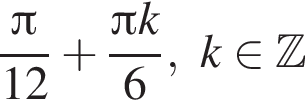
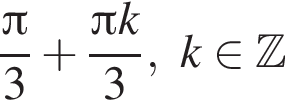
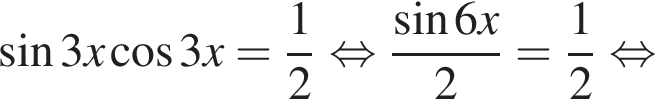
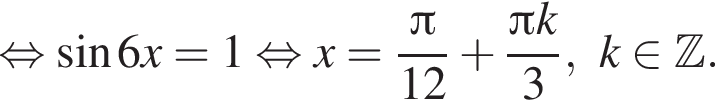
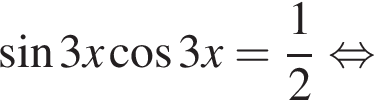
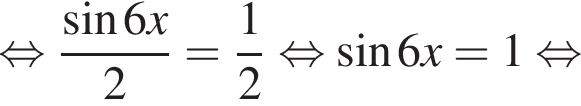
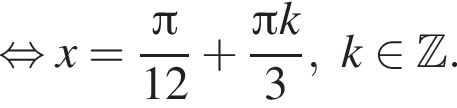
 проходящую через точку
проходящую через точку 
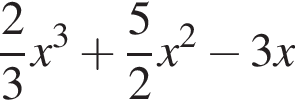
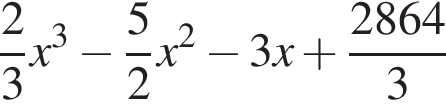
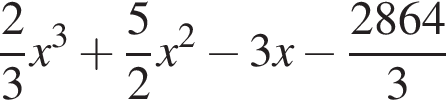
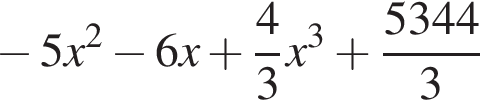
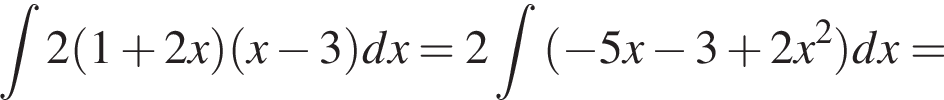
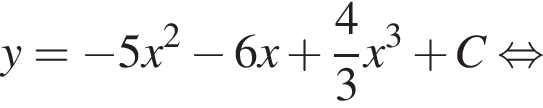
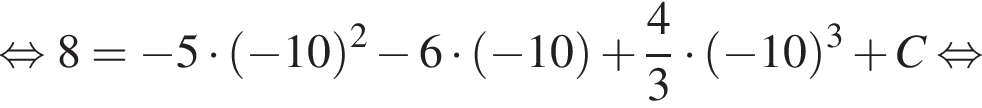
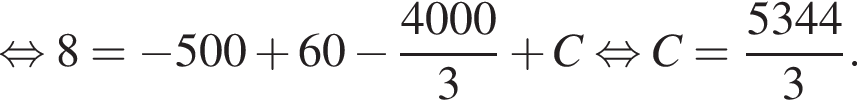
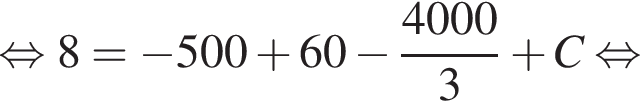
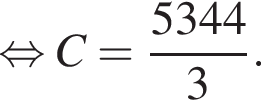
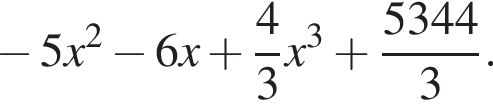
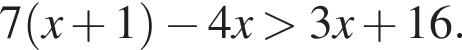
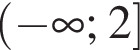
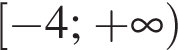
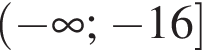

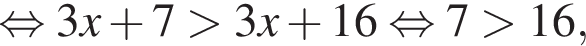
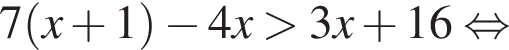
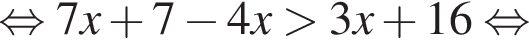
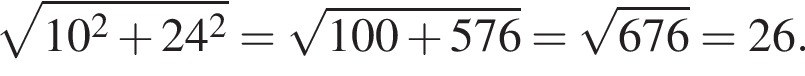


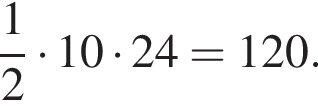 Значит, высота, проведенная к гипотенузе, равна
Значит, высота, проведенная к гипотенузе, равна 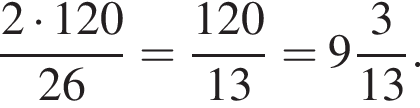

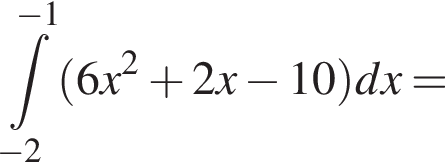
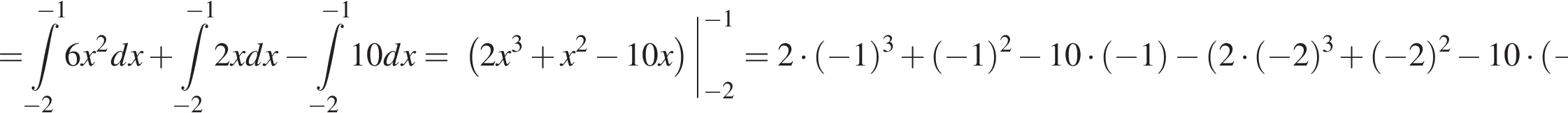
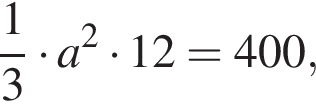 откуда
откуда 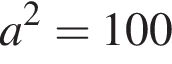 или
или 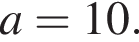 Полная поверхность состоит из квадрата площади
Полная поверхность состоит из квадрата площади  и четырех равнобедренных треугольников с основанием 10 и высотой, равной (см. рисунок)
и четырех равнобедренных треугольников с основанием 10 и высотой, равной (см. рисунок)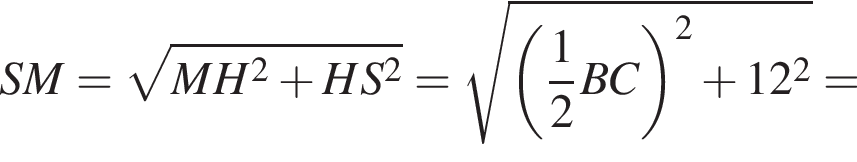
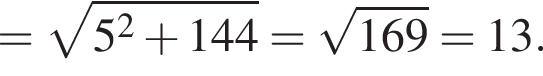

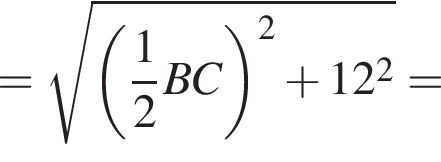
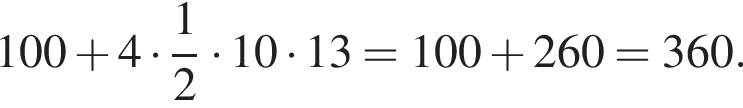
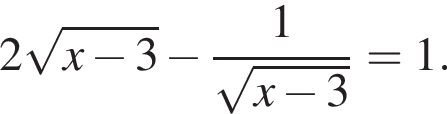
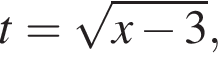
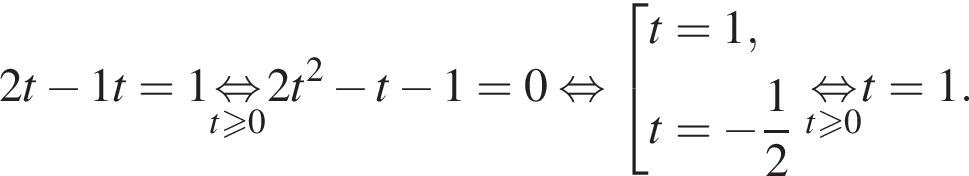
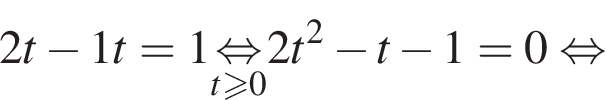
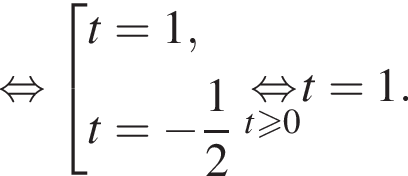
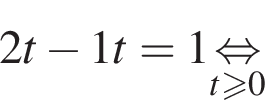
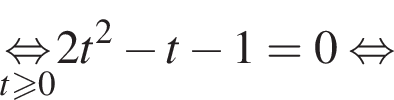
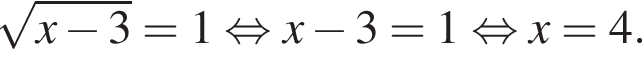
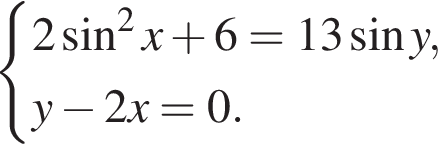
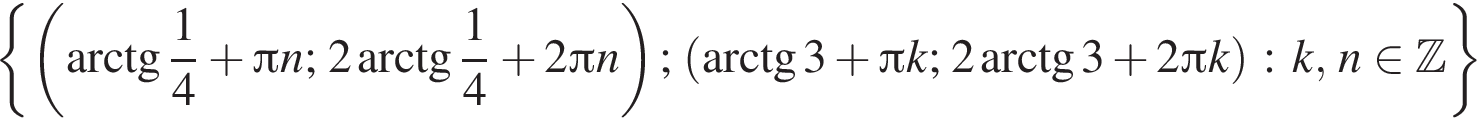
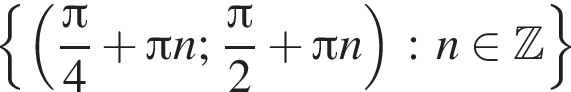
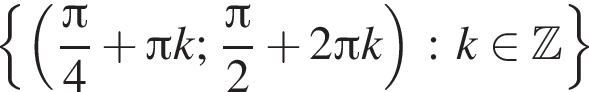

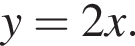 Подставляя это выражение в первое уравнение, находим
Подставляя это выражение в первое уравнение, находим

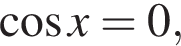 то уравнение сводится к
то уравнение сводится к 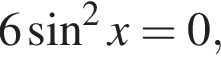 что невозможно при этом условии. Значит, таких корней нет и деление уравнения на
что невозможно при этом условии. Значит, таких корней нет и деление уравнения на 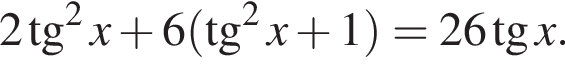
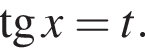

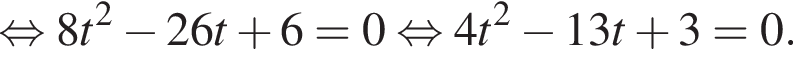
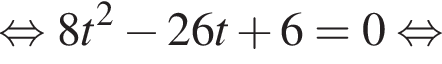
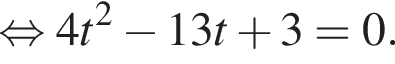

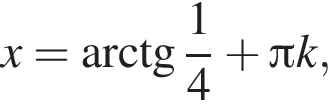
 и графиком ее производной.
и графиком ее производной.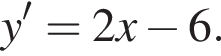 Найдем точки пересечения графиков функций y и y':
Найдем точки пересечения графиков функций y и y':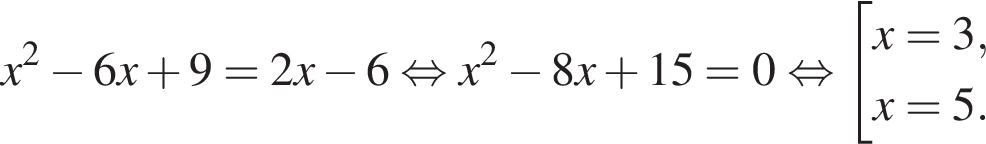
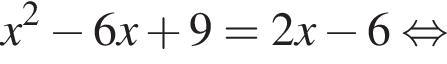
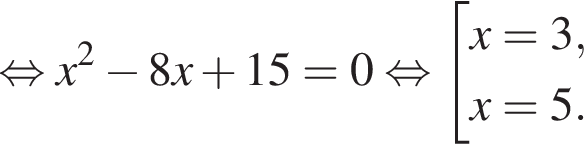
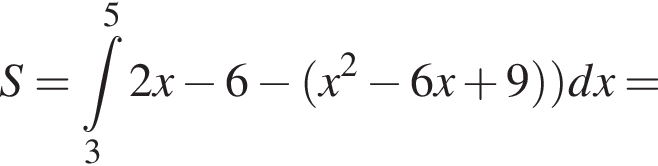
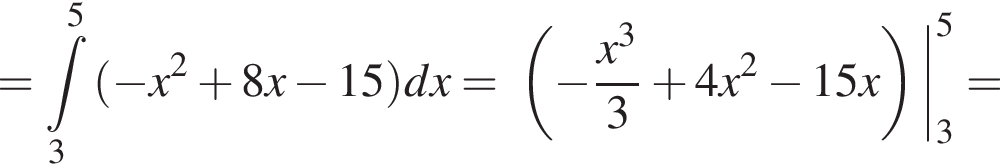
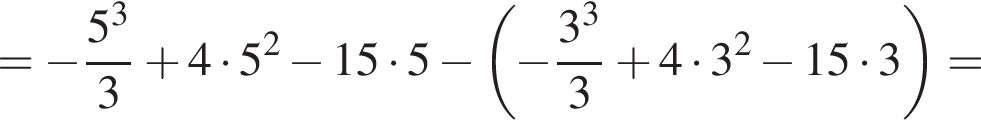
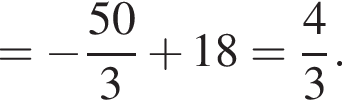
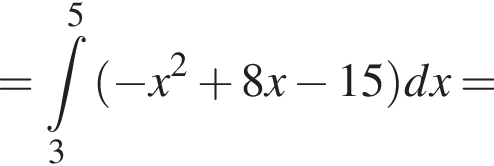
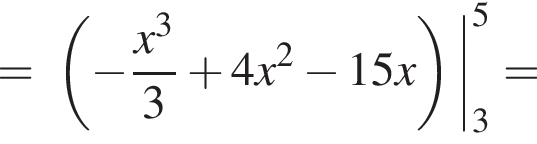
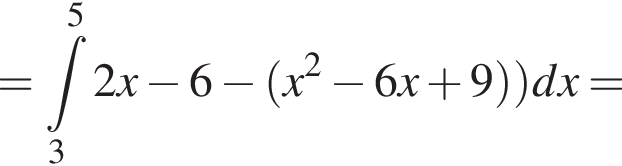
 Отношение
Отношение  По условию
По условию  откуда
откуда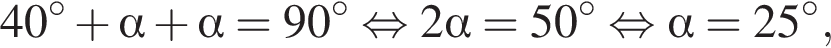
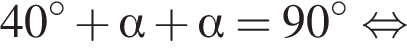
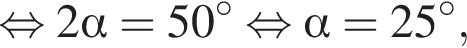
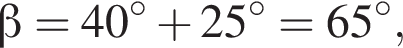
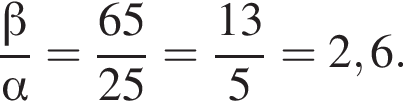
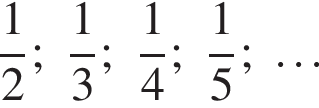
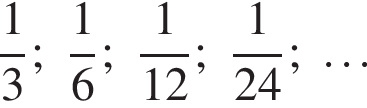
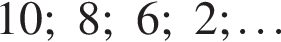
 и
и 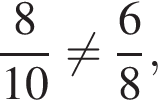
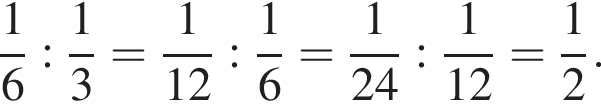
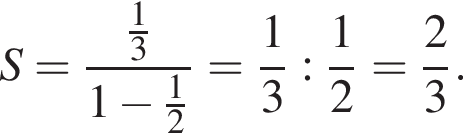
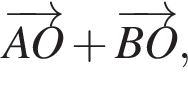
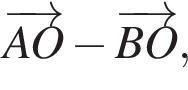
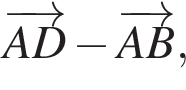 если AB = 8, BC = 6.
если AB = 8, BC = 6.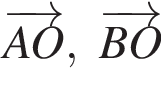 соответствует по длине отрезку AD, поэтому вектор
соответствует по длине отрезку AD, поэтому вектор 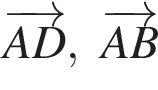 соответствует по длине отрезку BD, поэтому вектор
соответствует по длине отрезку BD, поэтому вектор 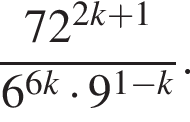
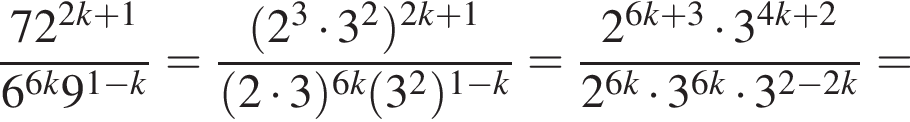
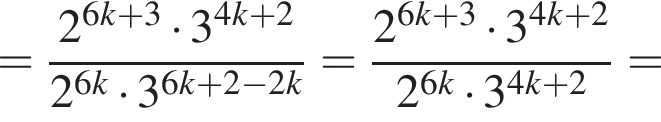
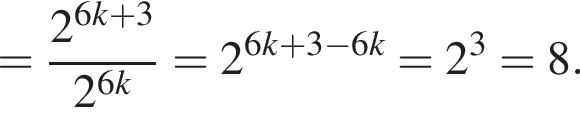
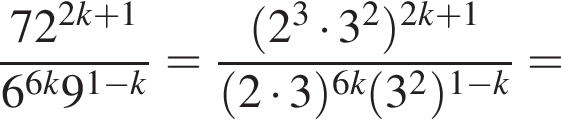
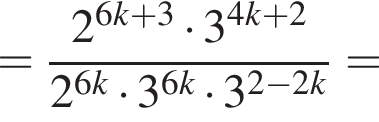
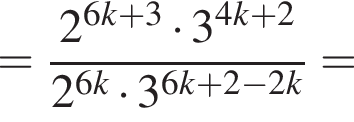
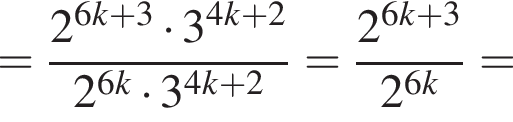
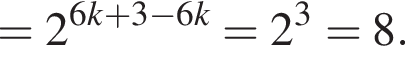
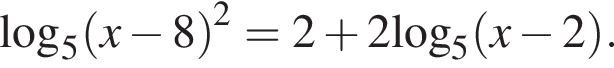
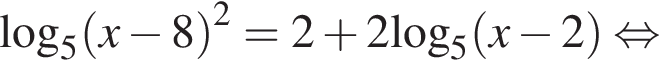

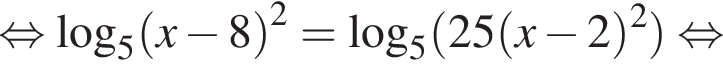
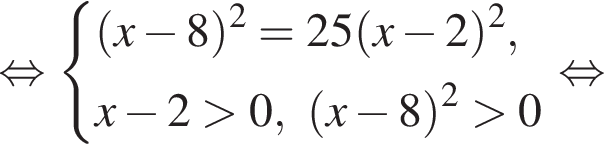
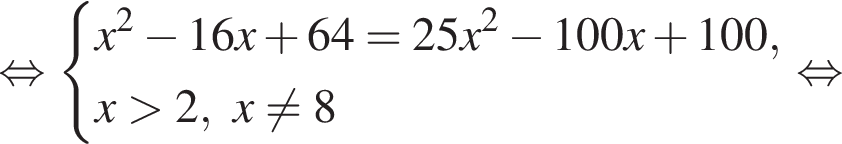
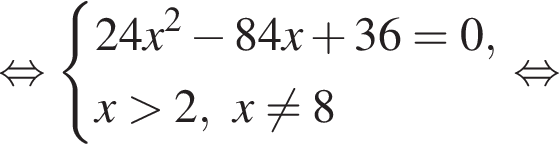
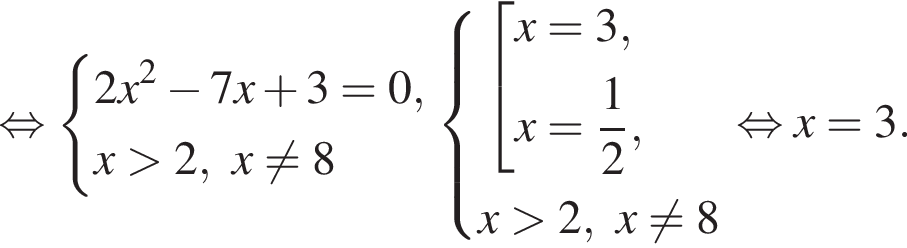

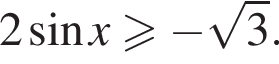
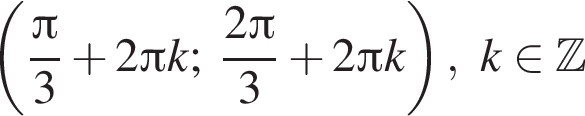
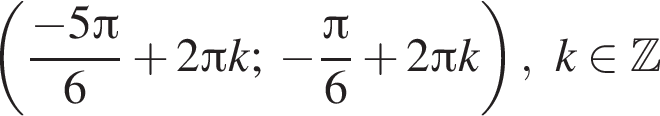
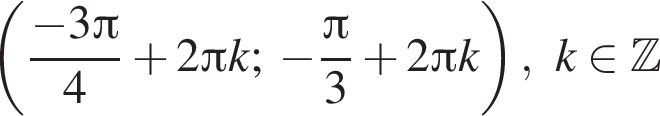
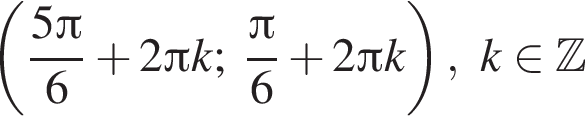
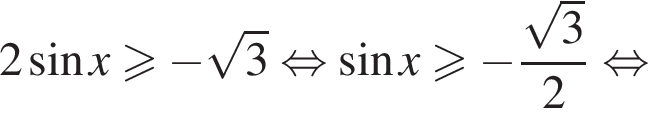
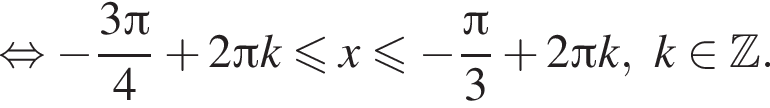
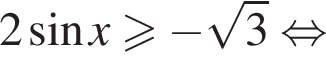
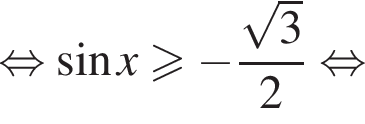
 в точке с абсциссой
в точке с абсциссой 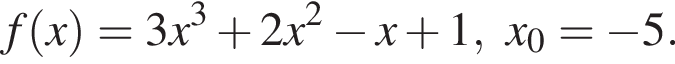

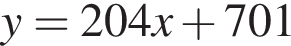
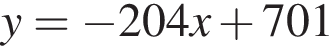
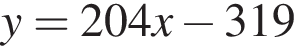
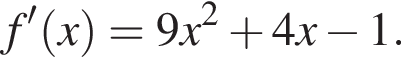 Составим уравнение касательной в точке x0 = −5:
Составим уравнение касательной в точке x0 = −5: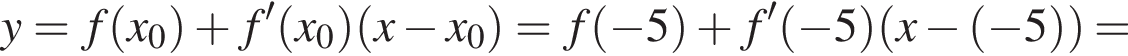
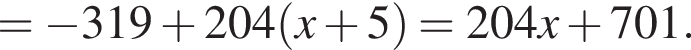
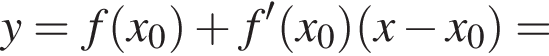
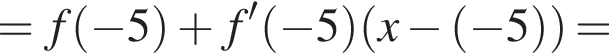
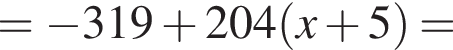
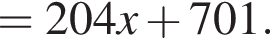
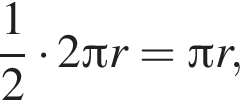 поэтому длины дуг равны 6π и 8π, значит, меньшая дуга составляет
поэтому длины дуг равны 6π и 8π, значит, меньшая дуга составляет 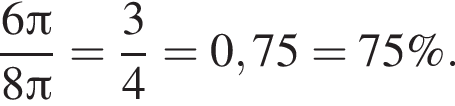
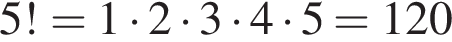 способами.
способами. 
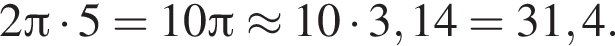

 вариантов, какие 3 карточки мог взять Марат, получаем
вариантов, какие 3 карточки мог взять Марат, получаем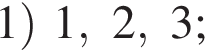
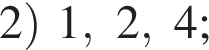
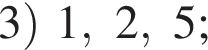

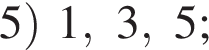
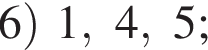
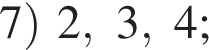
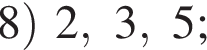
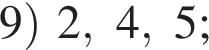
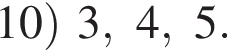
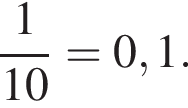
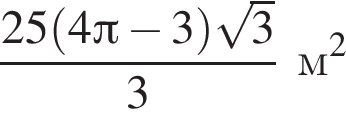
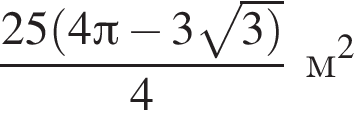
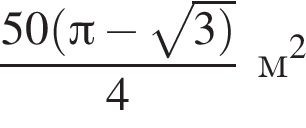
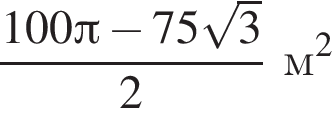
 площади сегментов в сумме равны
площади сегментов в сумме равны 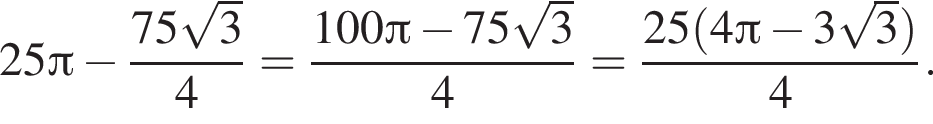
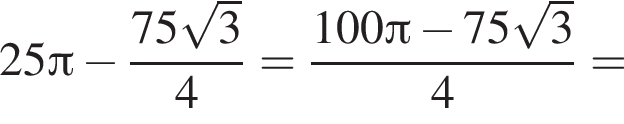
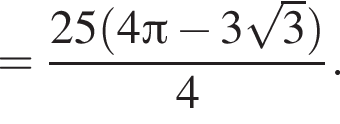
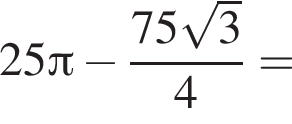
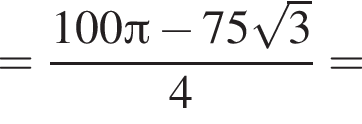
 Установите соответствие между наибольшим и наименьшим значениями функции и их числовыми значениями.
Установите соответствие между наибольшим и наименьшим значениями функции и их числовыми значениями.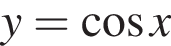 — промежуток [−1; 1]. Тогда область допустимых значений функции
— промежуток [−1; 1]. Тогда область допустимых значений функции  — промежуток [−3; −5]. Наибольшее значение функции равно −3, наименьшее значение функции равно −5.
— промежуток [−3; −5]. Наибольшее значение функции равно −3, наименьшее значение функции равно −5.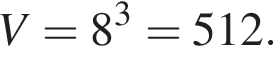 Найдем площадь полной поверхности куба:
Найдем площадь полной поверхности куба: 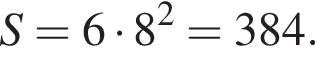
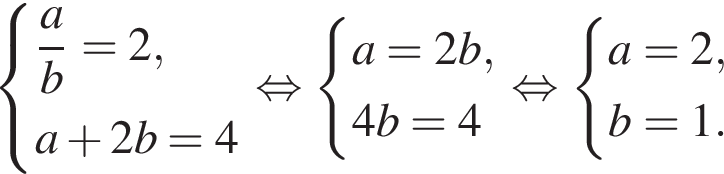
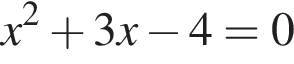 и
и 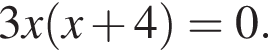 Установите соответствия:
Установите соответствия: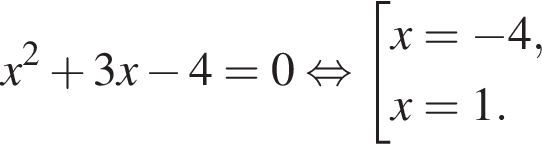
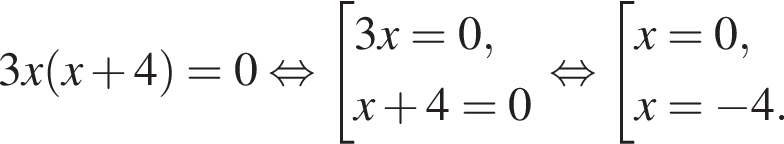
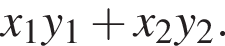
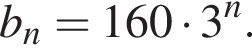 Установите соответствие между выражением и его числовым значением.
Установите соответствие между выражением и его числовым значением.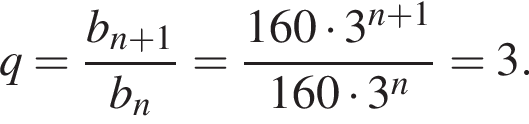
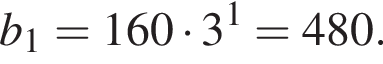 Сумма первых k членов геометрической прогрессии может быть найдена по формуле:
Сумма первых k членов геометрической прогрессии может быть найдена по формуле: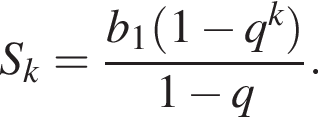
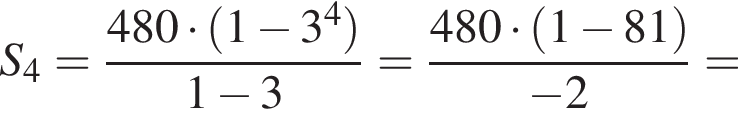
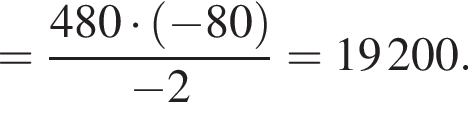
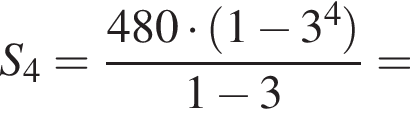
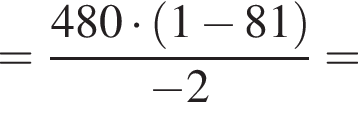
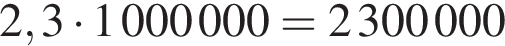 сантиметров, то есть 23 000 метров или 23 километра. Подходят ответы 2 и 6.
сантиметров, то есть 23 000 метров или 23 километра. Подходят ответы 2 и 6.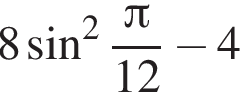 равно
равно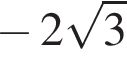
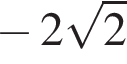
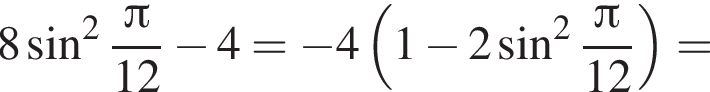
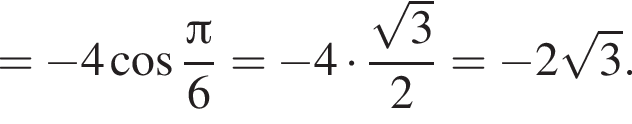
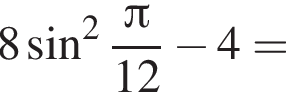
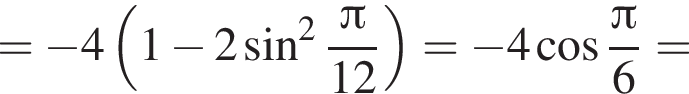
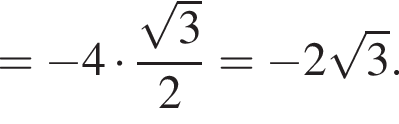
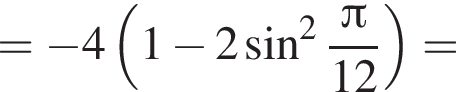
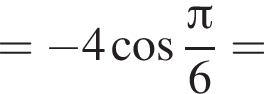
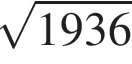

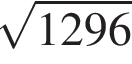


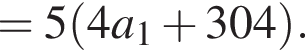
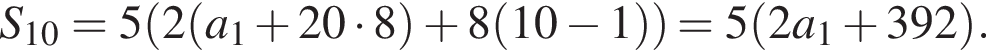
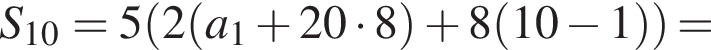
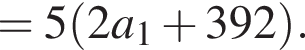
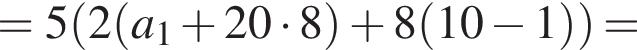

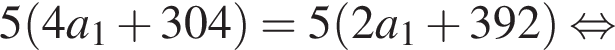
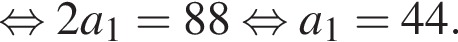
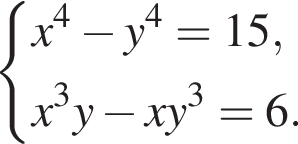
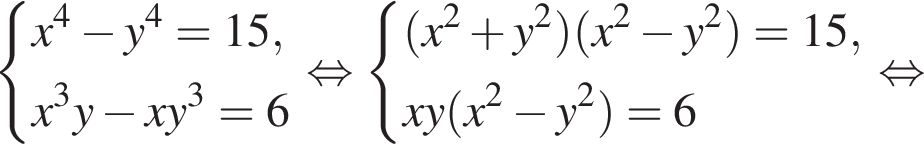
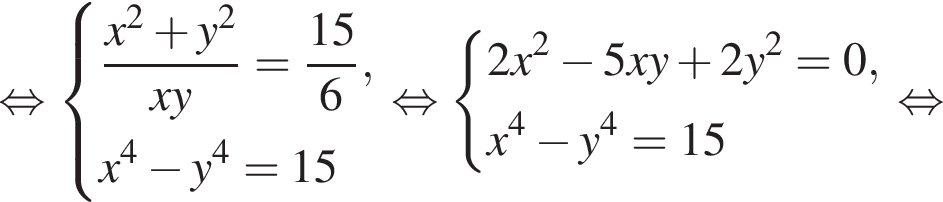
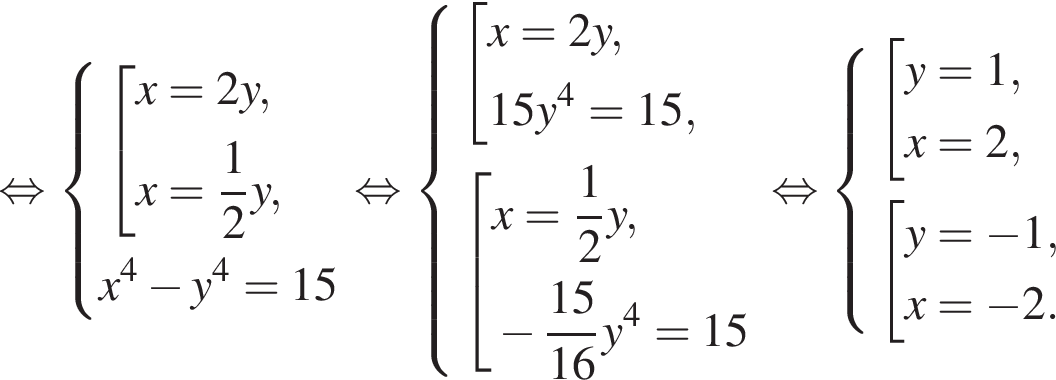
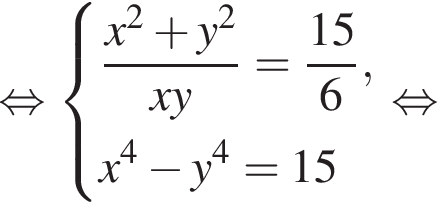
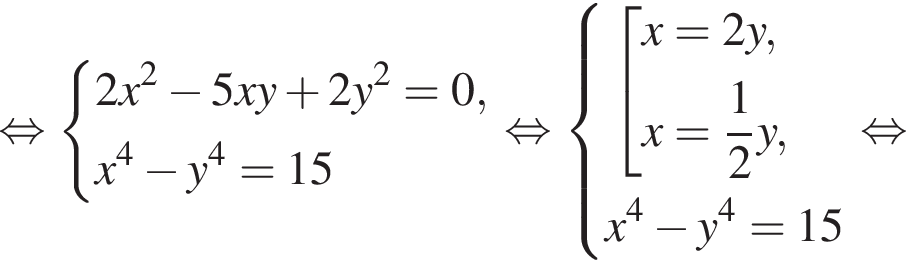
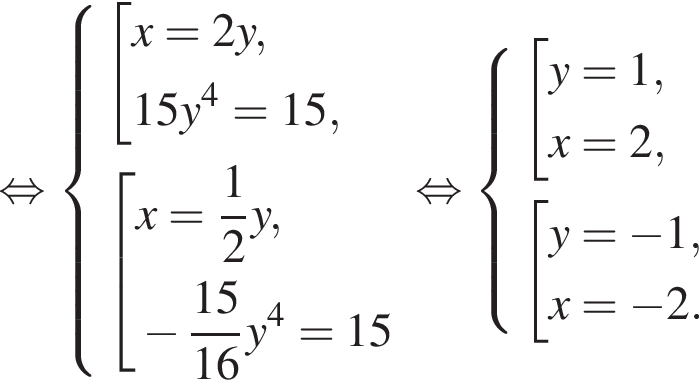

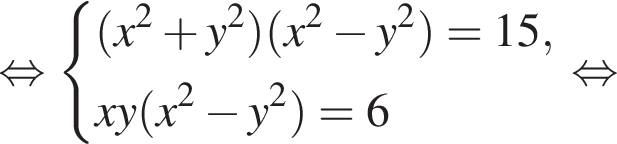
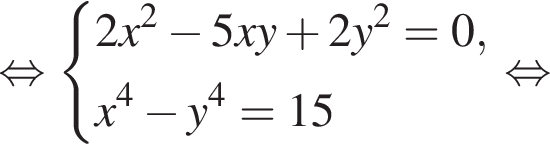
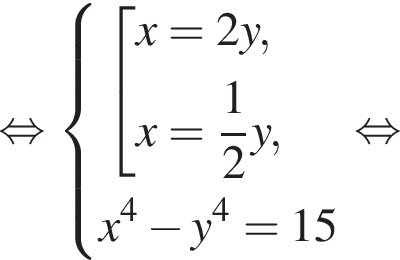
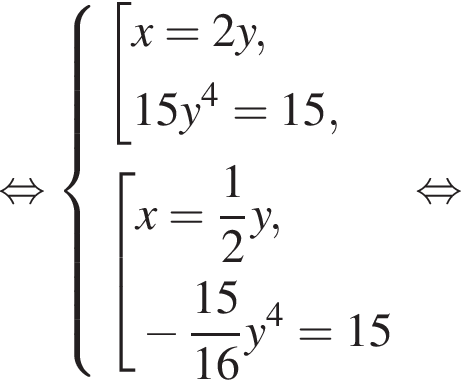
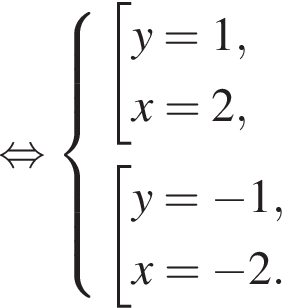
 равно 4.
равно 4.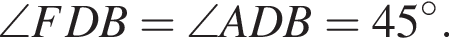 С другой стороны, проекция F на плоскость основания лежит на BD, следовательно, BD — проекция FD и найденный нами угол и есть угол между прямой и плоскостью. Этому выражению равны ответы 1 и 4, просто по-разному записаны.
С другой стороны, проекция F на плоскость основания лежит на BD, следовательно, BD — проекция FD и найденный нами угол и есть угол между прямой и плоскостью. Этому выражению равны ответы 1 и 4, просто по-разному записаны.