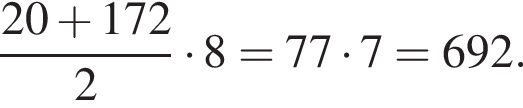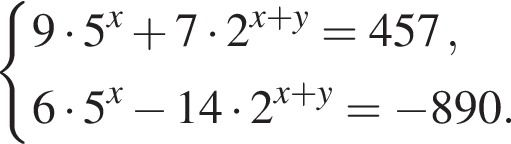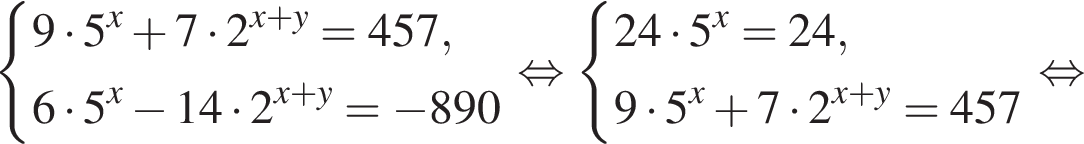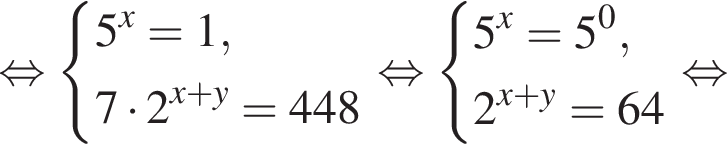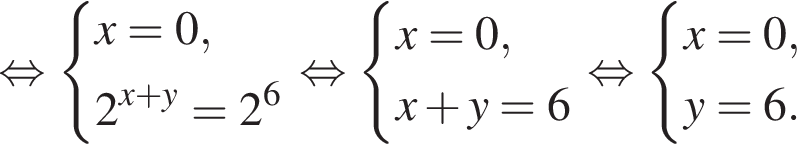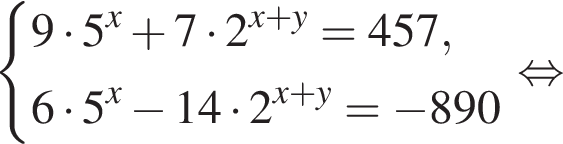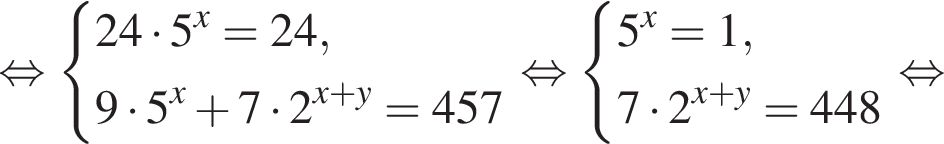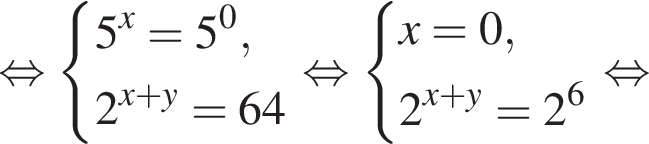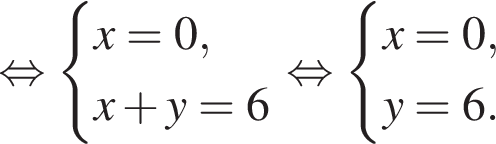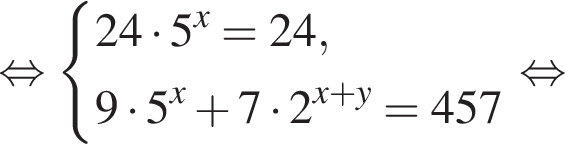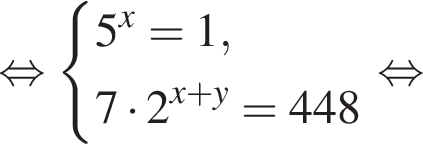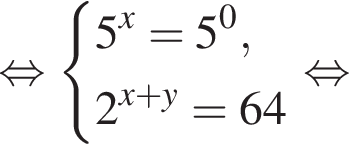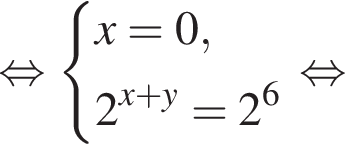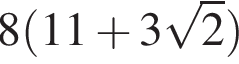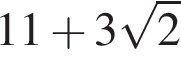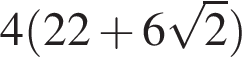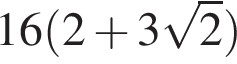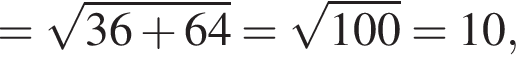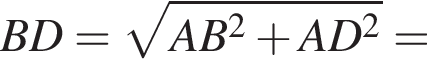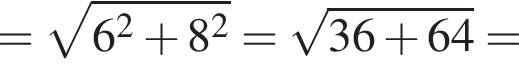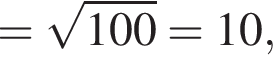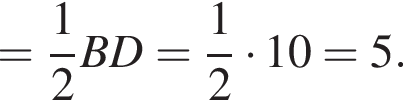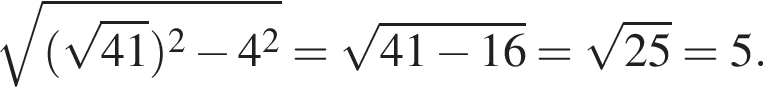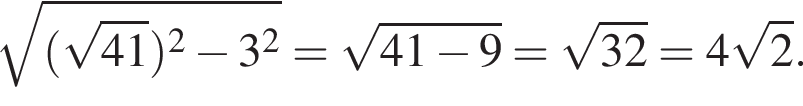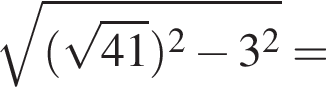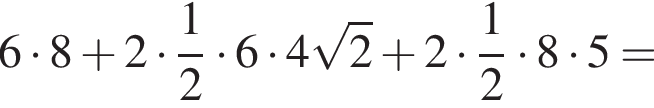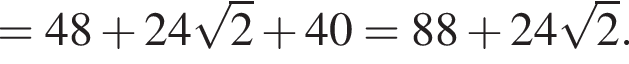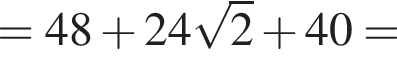1. Тип 1 № 2512 

Источник: Реальная версия ЕНТ по математике 2021 года, вариант 4222. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.13\. Комбинированные задания, 1\.4\. Вычисление степей и корней, 1\.6\. Вычисление логарифмов
Числовые алгебраические выражения. Задания для подготовки
i
Вычислите: 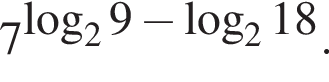
1) 1
2) 7
3) 
4) 
Решение. Вычислим:
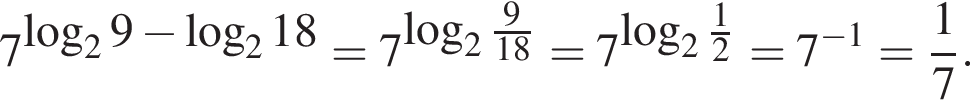
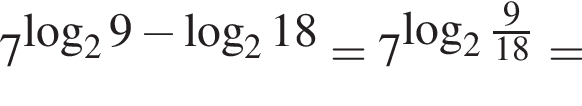
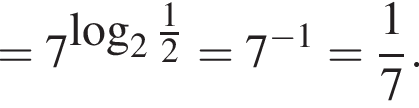
Правильный ответ указан под номером 4.
Ответ: 4
2512
4
Источник: Реальная версия ЕНТ по математике 2021 года, вариант 4222. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
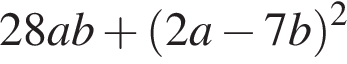 при
при 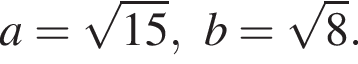
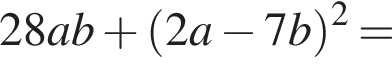
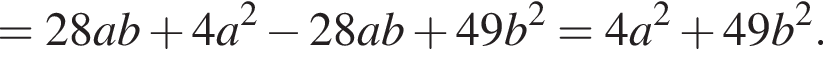
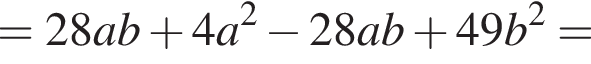
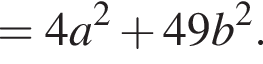
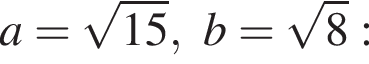
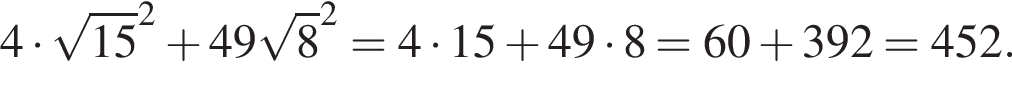
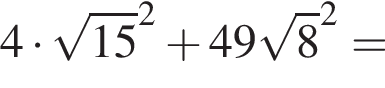



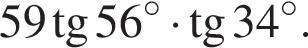

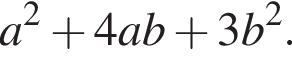
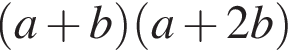
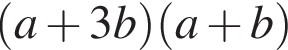

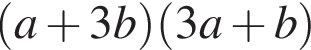
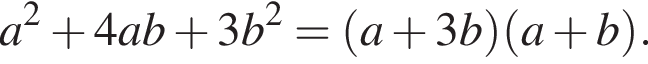
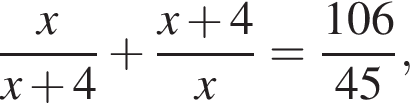
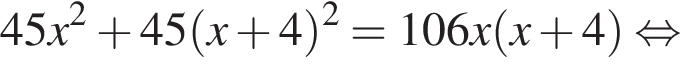
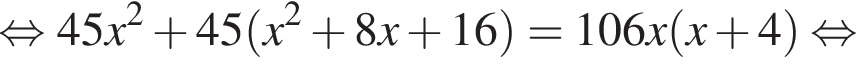
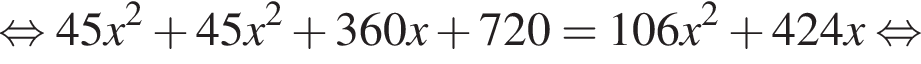
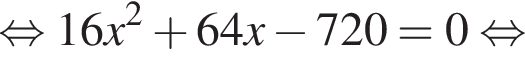

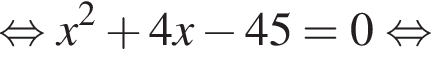
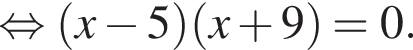
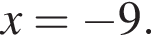 Видимо имеется в виду, что дробь равна
Видимо имеется в виду, что дробь равна 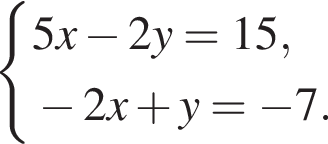
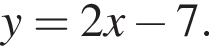 Подставляя это выражение в первое уравнение, получаем
Подставляя это выражение в первое уравнение, получаем 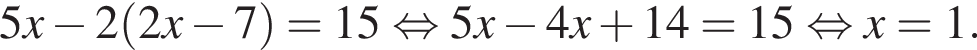
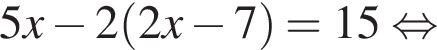
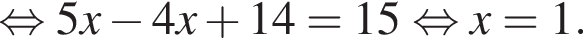
 Итого, ответ (1; −5).
Итого, ответ (1; −5).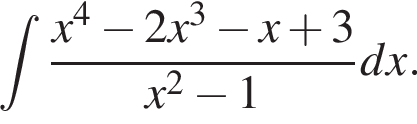
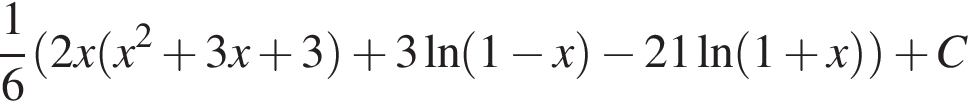



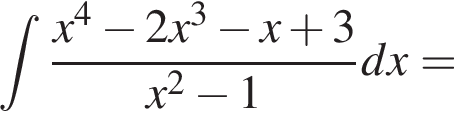
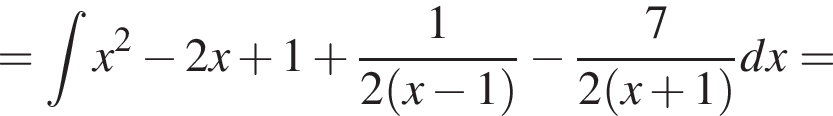
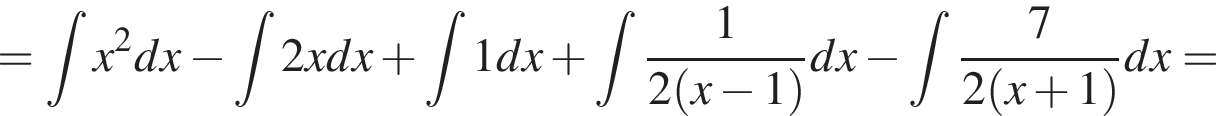
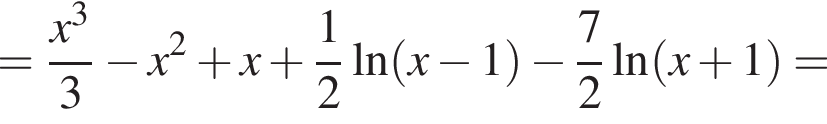
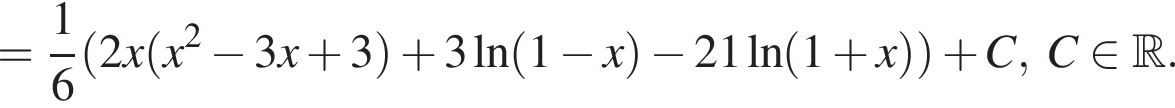
 по условию
по условию  а
а 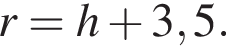 Тогда
Тогда
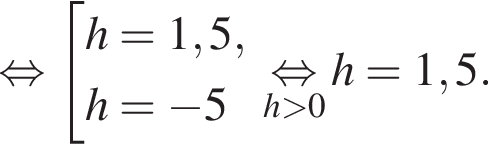

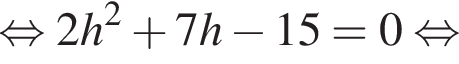
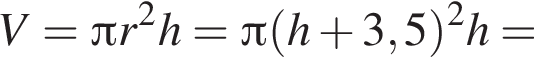
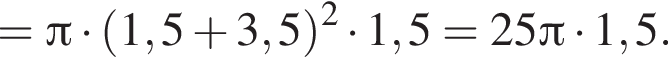


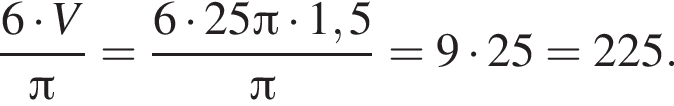
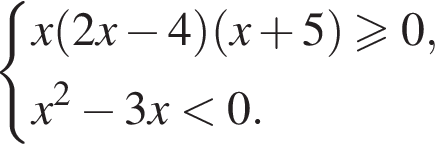
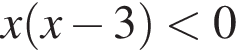 и решим его методом интервалов. Ответом будет
и решим его методом интервалов. Ответом будет  При таких x множители x и
При таких x множители x и 
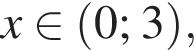 получаем
получаем 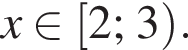
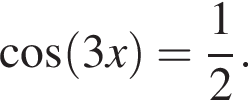
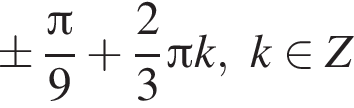
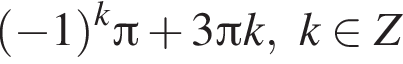

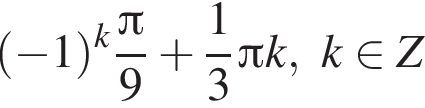
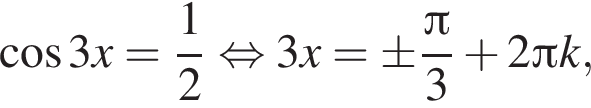
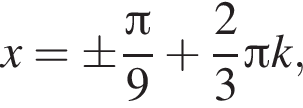
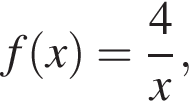 при
при 

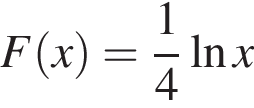
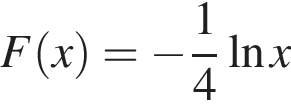
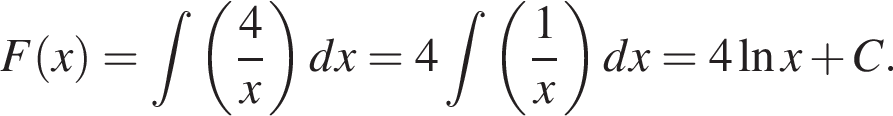
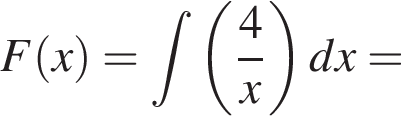
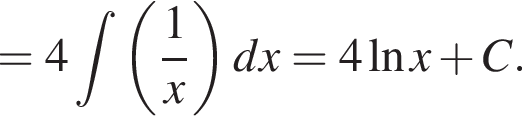
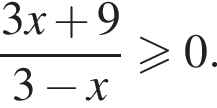

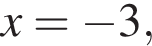 корнем знаменателя
корнем знаменателя 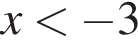 числитель и знаменатель имеют разные знаки (такие x не подходят), при
числитель и знаменатель имеют разные знаки (такие x не подходят), при  числитель и знаменатель оба положительны (такие x подходят), при
числитель и знаменатель оба положительны (такие x подходят), при  дробь равна нулю, а при
дробь равна нулю, а при 
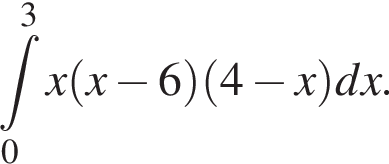
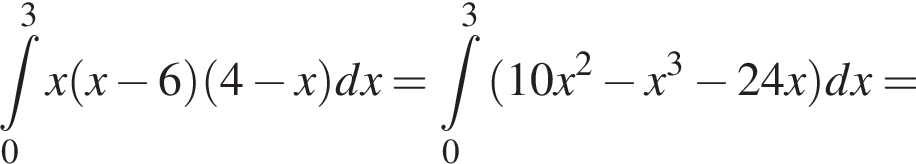
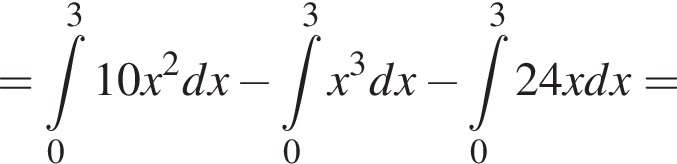
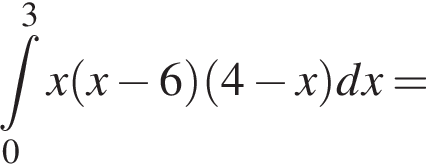
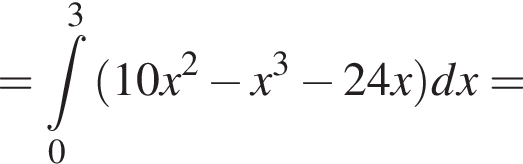
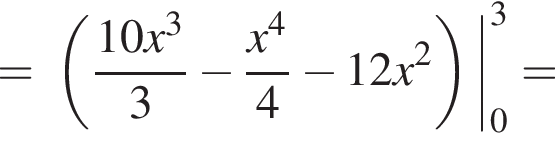
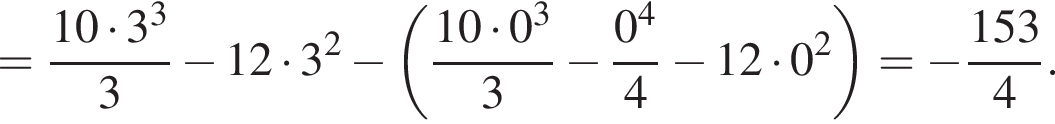
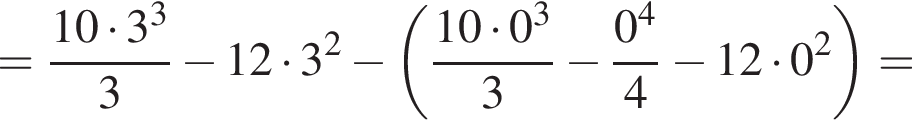
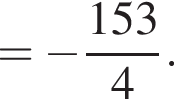
 и
и 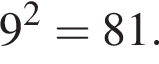 Тогда объем усеченной пирамиды равен
Тогда объем усеченной пирамиды равен 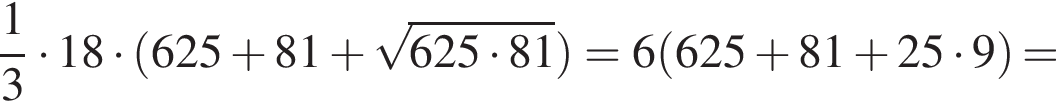

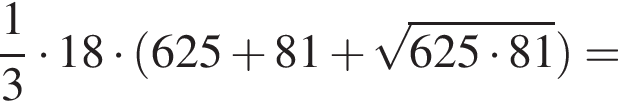
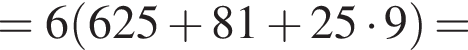
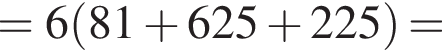
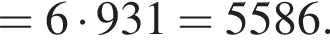
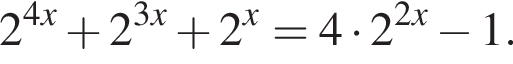
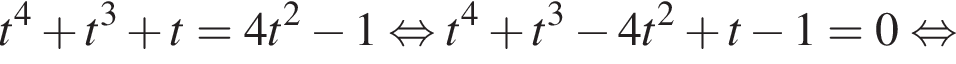
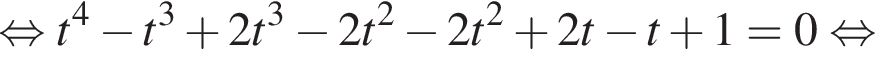
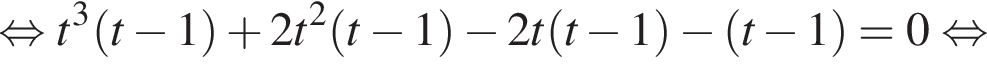
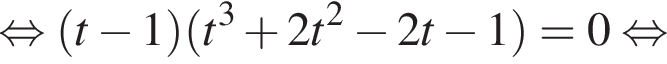
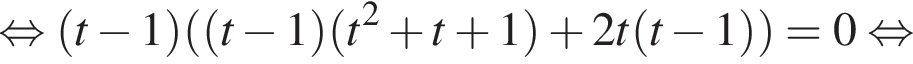
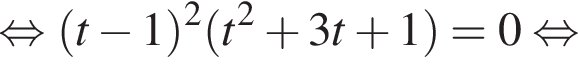
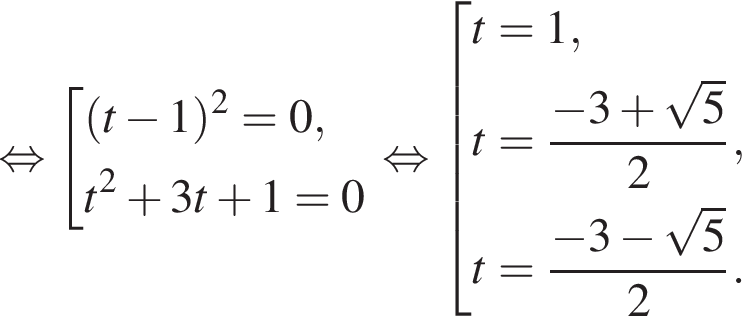

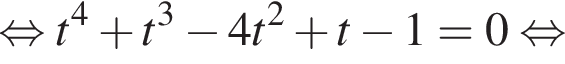
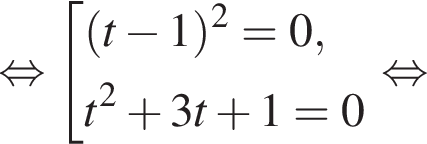
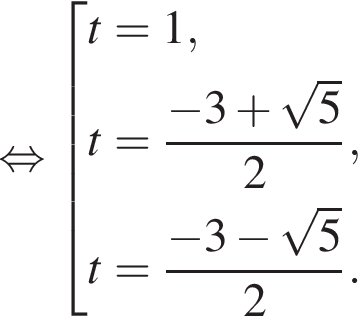
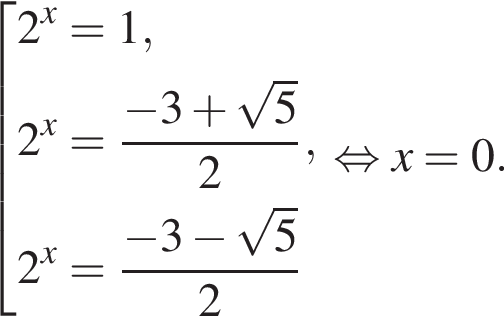
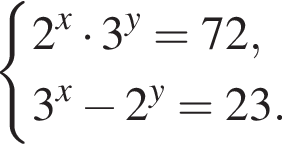
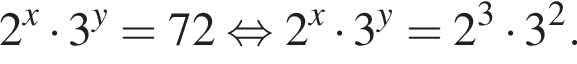
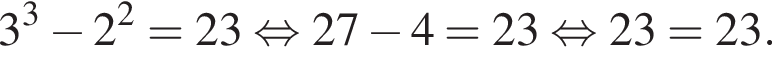
 и графиком ее производной.
и графиком ее производной.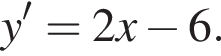 Найдем точки пересечения графиков функций y и y':
Найдем точки пересечения графиков функций y и y':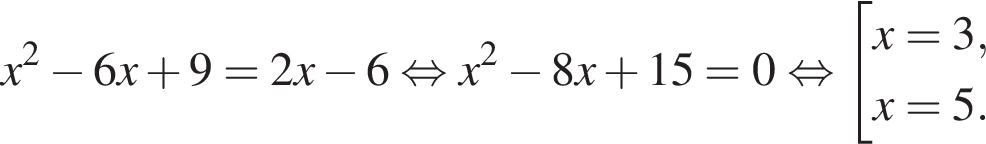
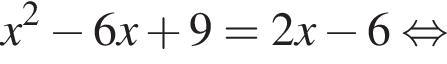
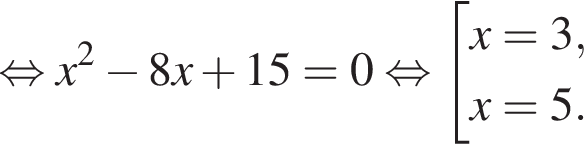
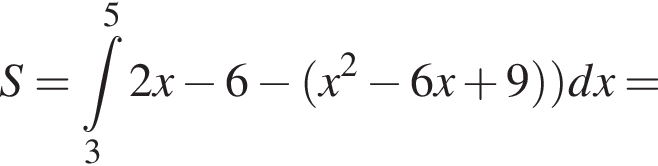
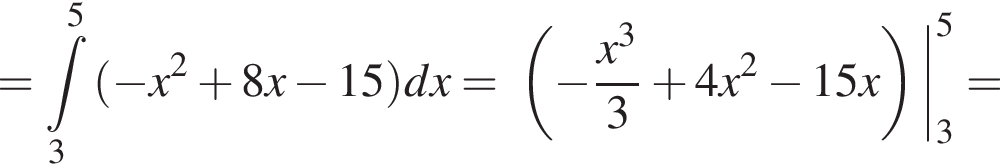
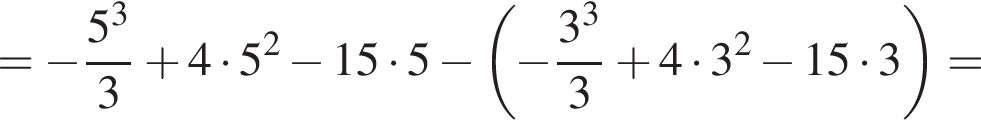
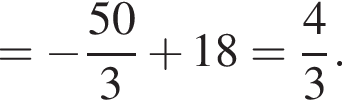
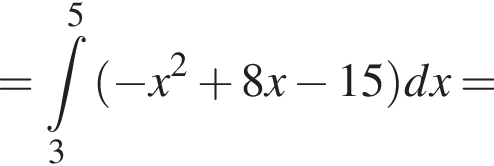
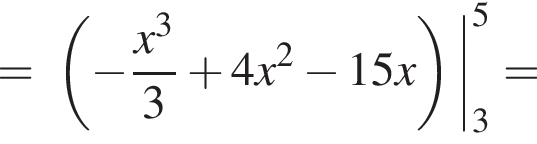
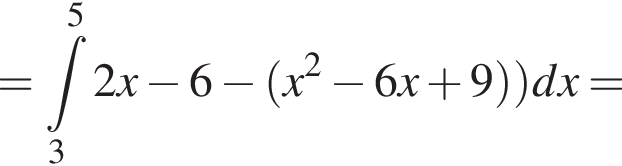
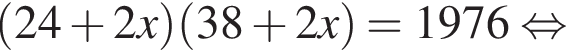
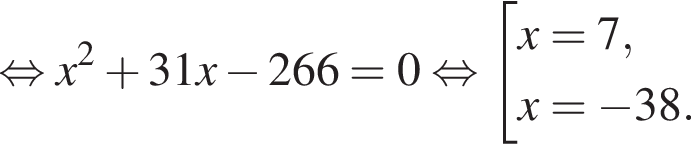
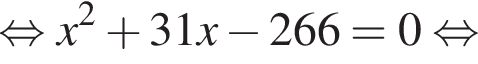
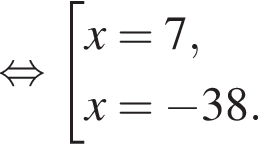
 тогда
тогда 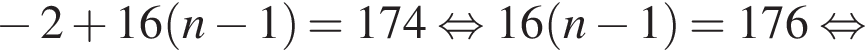
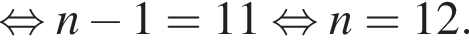
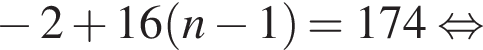
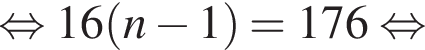
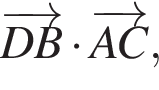 б)
б) 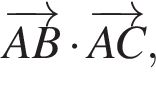 в)
в) 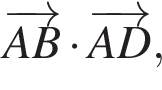 если
если 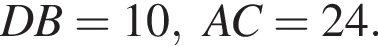

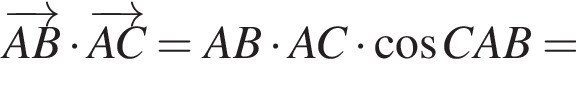
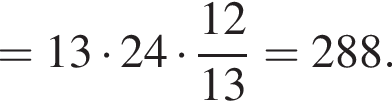
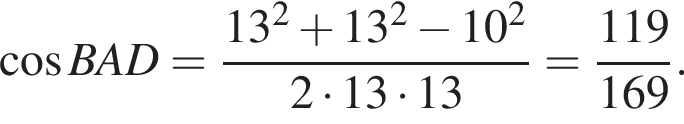



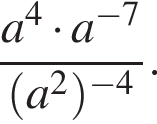
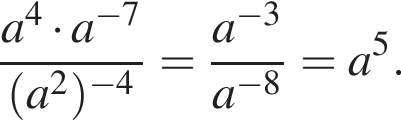


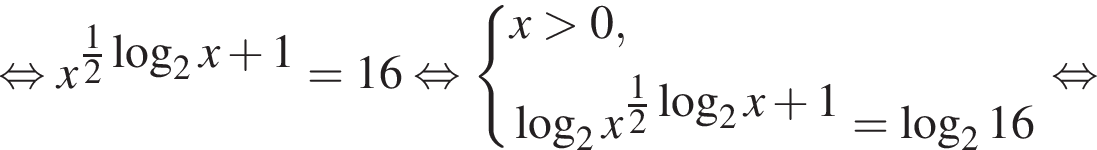
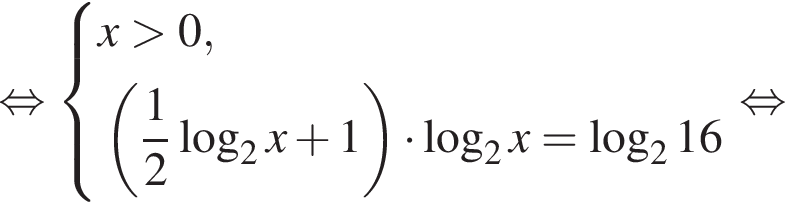
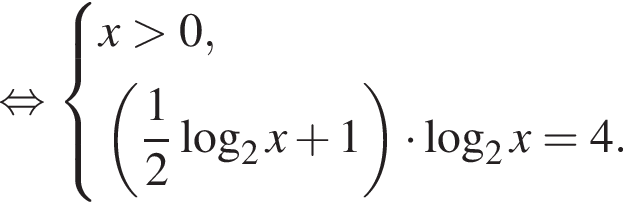
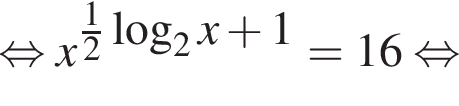
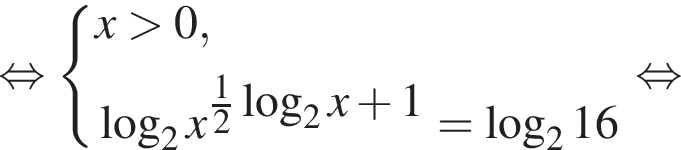

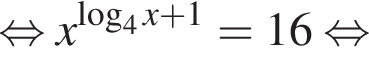
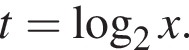 Тогда:
Тогда: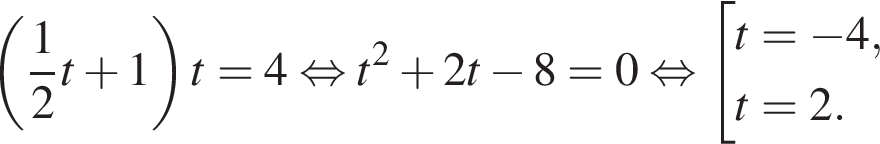
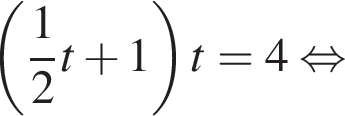
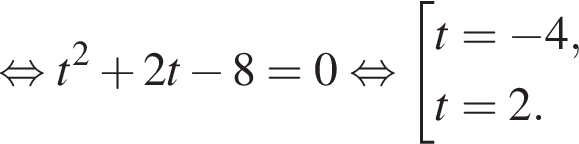
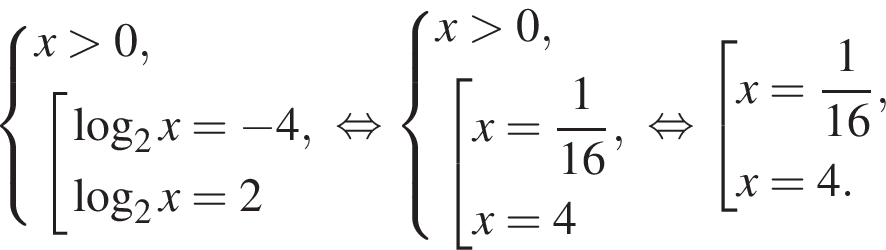
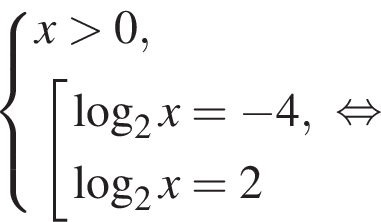
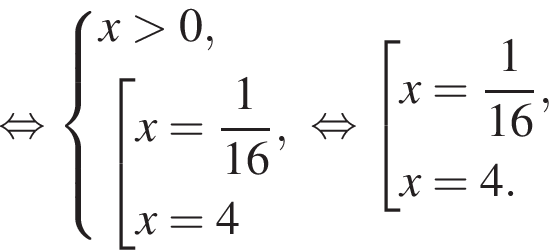
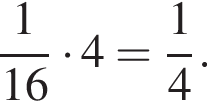
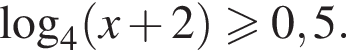
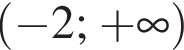

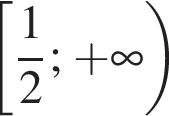

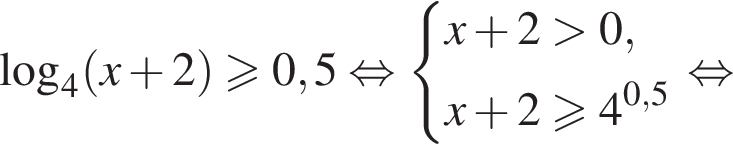
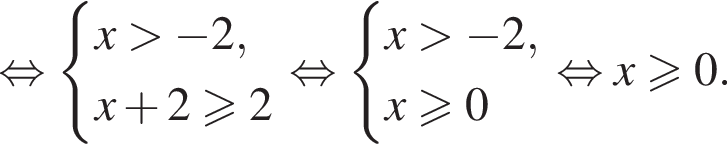
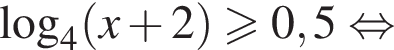
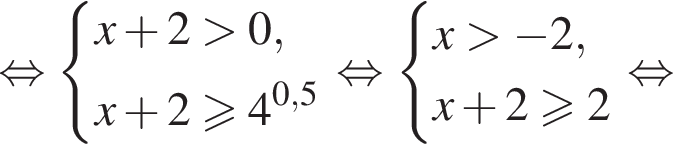
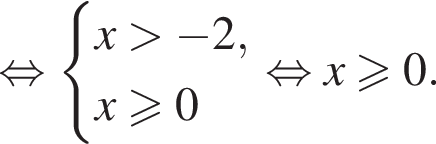
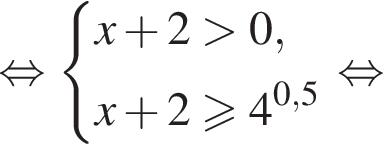
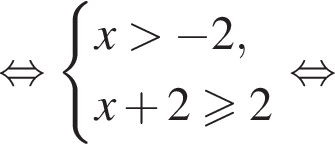
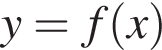 в точке с абсциссой
в точке с абсциссой 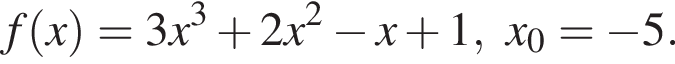

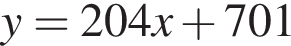
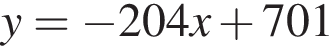
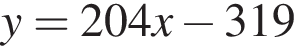
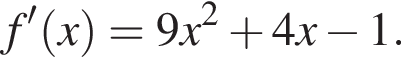 Составим уравнение касательной в точке x0 = −5:
Составим уравнение касательной в точке x0 = −5: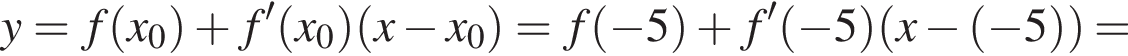
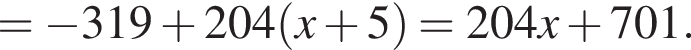
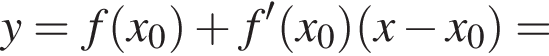
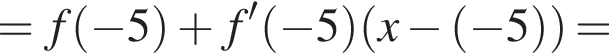
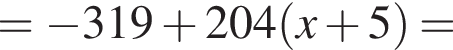
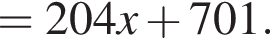
 над горизонтальной координатной плоскостью, значит, ее z-координата равна 4. Остальные ее координаты совпадают с координатами точки D, поэтому ответ (4; 4; 4).
над горизонтальной координатной плоскостью, значит, ее z-координата равна 4. Остальные ее координаты совпадают с координатами точки D, поэтому ответ (4; 4; 4).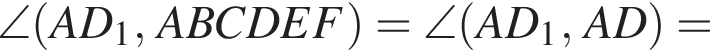

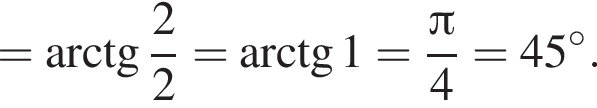
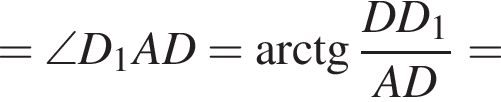
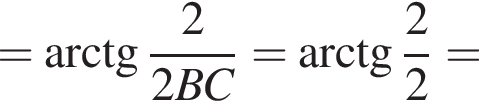
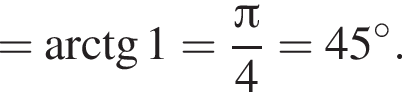
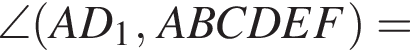

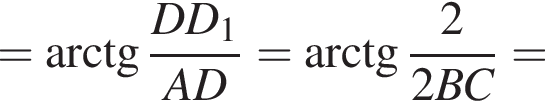
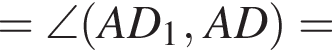
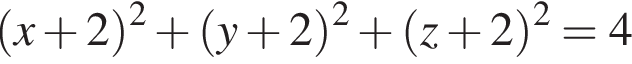
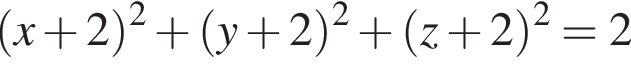
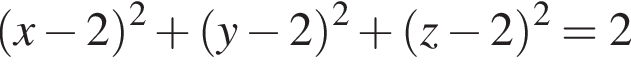
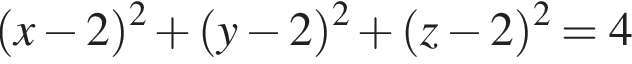
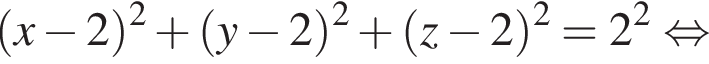
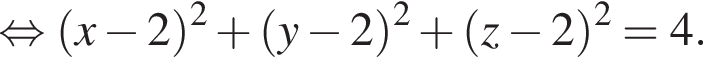
 Установите соответствие между наибольшим и наименьшим значениями функции и их числовыми значениями.
Установите соответствие между наибольшим и наименьшим значениями функции и их числовыми значениями.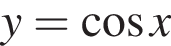 — [−1; 1]. Тогда область допустимых значений функции
— [−1; 1]. Тогда область допустимых значений функции 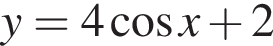 — [−2; 6]. Наибольшее значение функции равно 6, наименьшее значение функции равно −2.
— [−2; 6]. Наибольшее значение функции равно 6, наименьшее значение функции равно −2.
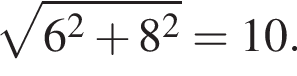
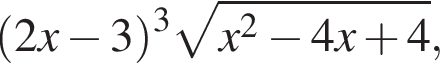 если известно, что
если известно, что 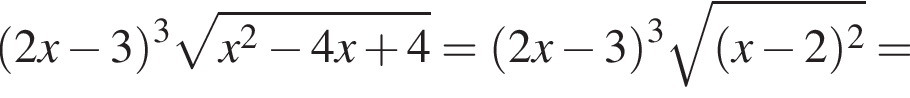

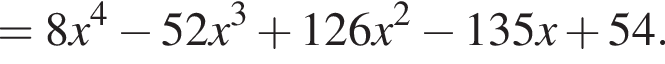
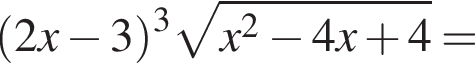

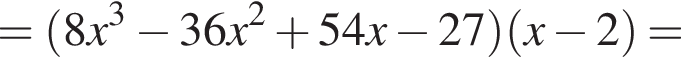
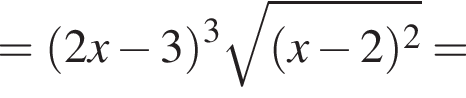
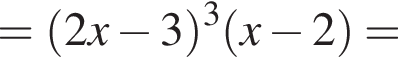
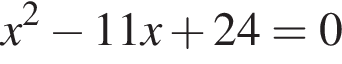 и
и 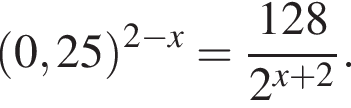 Установите соответствия:
Установите соответствия:
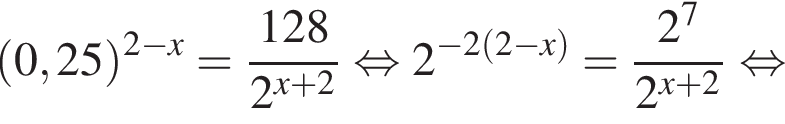
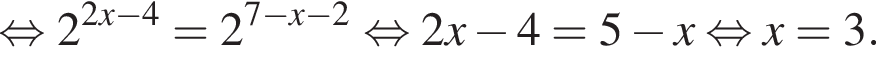
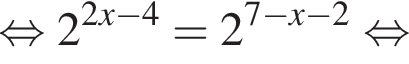
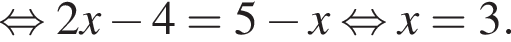
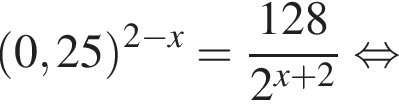
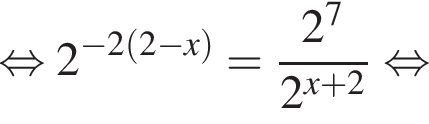
 Установите соответствие между выражением и его числовым значением.
Установите соответствие между выражением и его числовым значением.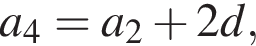 откуда
откуда 
 также
также 


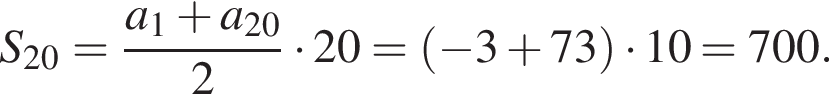
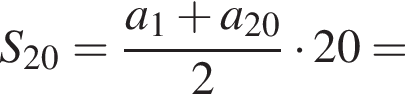
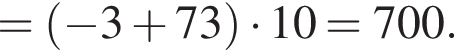

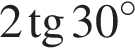
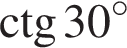
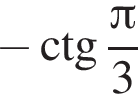
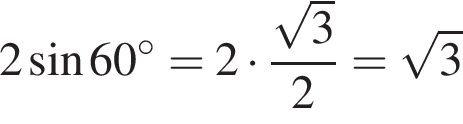 и
и 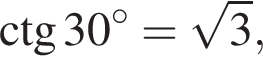
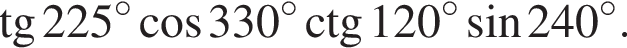
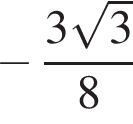
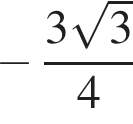

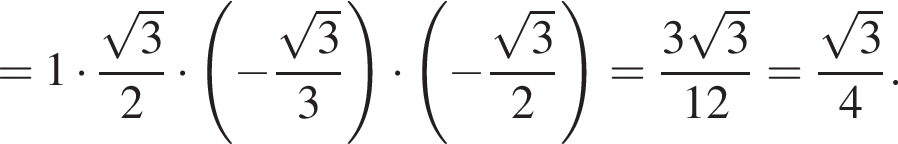
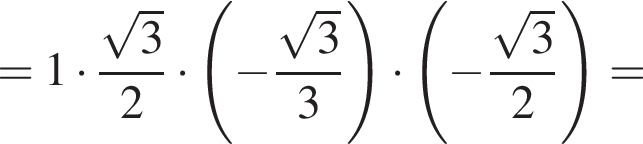
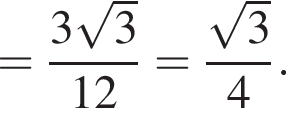
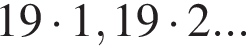 Выпишем эти числа до 149 и сразу прибавим единицу. Получим числа 20, 39, 58, 77, 96, 115, 134, 153 (а число 172 уже слишком велико). Сумма этих восьми чисел составляет
Выпишем эти числа до 149 и сразу прибавим единицу. Получим числа 20, 39, 58, 77, 96, 115, 134, 153 (а число 172 уже слишком велико). Сумма этих восьми чисел составляет